The characteristic equation of A = [[3, 10, 5], [-2, -3, -4], [3, 5, 7]]
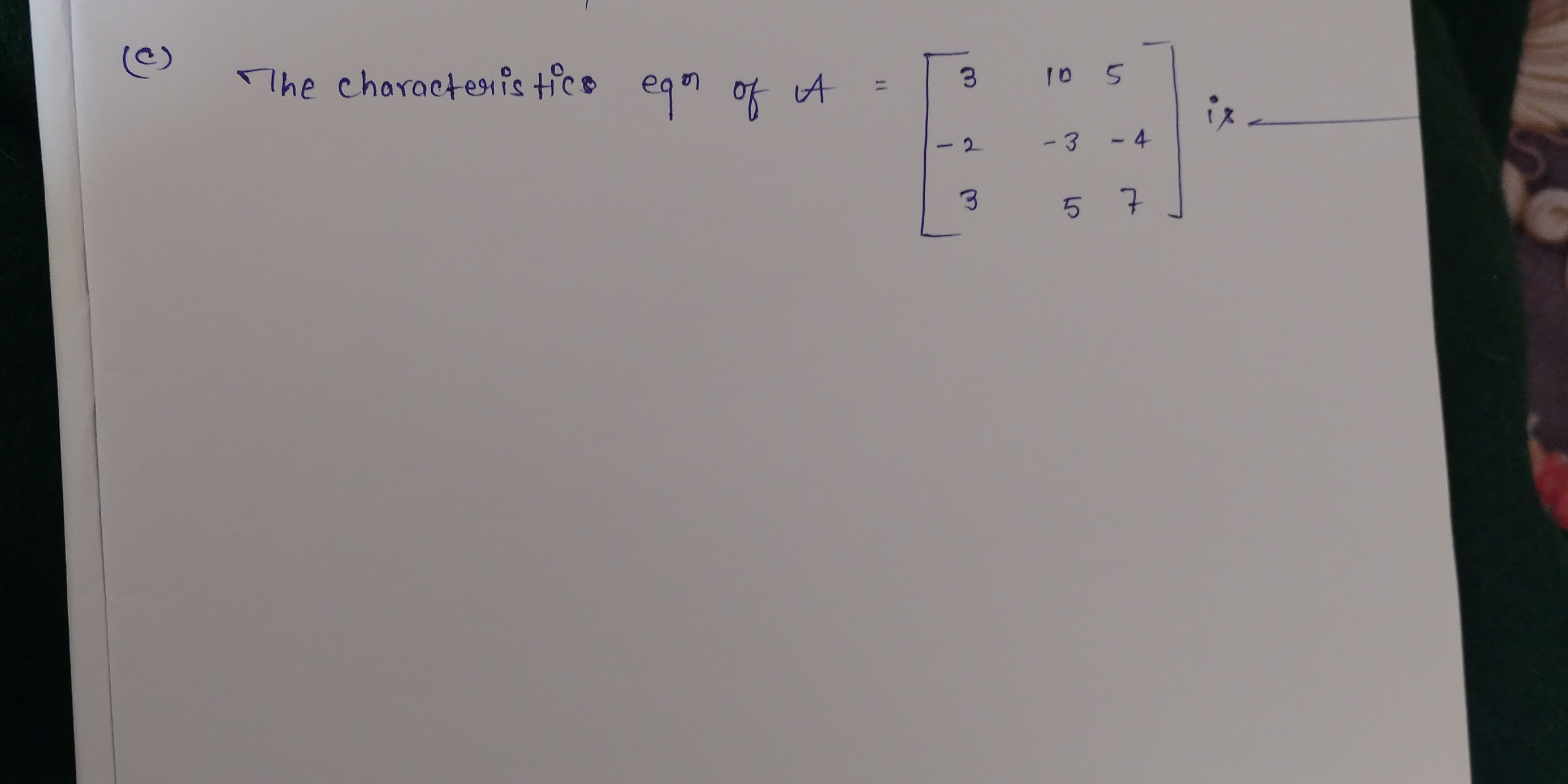
Understand the Problem
The question is asking for the characteristic equation of a given matrix. To solve this, we will need to compute the determinant of the matrix formed by subtracting lambda times the identity matrix from the given matrix.
Answer
The characteristic equation is given by: $$ -\lambda^3 + 7\lambda^2 + 20\lambda - 18 = 0 $$
Answer for screen readers
The characteristic equation of the matrix ( A ) is:
$$ -\lambda^3 + 7\lambda^2 + 20\lambda - 18 = 0 $$
Steps to Solve
- Define the matrix and the identity matrix
Given the matrix ( A = \begin{bmatrix} 3 & 10 & 5 \ -2 & -3 & -4 \ 3 & 5 & 7 \end{bmatrix} )
The identity matrix ( I ) of size ( 3 ) is ( I = \begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{bmatrix} ).
- Construct the matrix ( A - \lambda I )
To find the characteristic equation, we subtract ( \lambda ) times the identity matrix from ( A ):
[ A - \lambda I = \begin{bmatrix} 3 - \lambda & 10 & 5 \ -2 & -3 - \lambda & -4 \ 3 & 5 & 7 - \lambda \end{bmatrix} ]
- Calculate the determinant of ( A - \lambda I )
We need to find the determinant of the resulting matrix:
[ \text{det}(A - \lambda I) = \begin{vmatrix} 3 - \lambda & 10 & 5 \ -2 & -3 - \lambda & -4 \ 3 & 5 & 7 - \lambda \end{vmatrix} ]
Using the determinant formula for a ( 3 \times 3 ) matrix:
[ \text{det}(A) = a(ei - fh) - b(di - fg) + c(dh - eg) ]
We apply this to the matrix elements.
- Expand the determinant
Let’s denote:
- ( a = 3 - \lambda )
- ( b = 10 )
- ( c = 5 )
- ( d = -2 )
- ( e = -3 - \lambda )
- ( f = -4 )
- ( g = 3 )
- ( h = 5 )
- ( i = 7 - \lambda )
The determinant expands as follows:
[ \text{det}(A - \lambda I) = (3 - \lambda)((-3 - \lambda)(7 - \lambda) - (-4)(5)) - 10((-2)(7 - \lambda) - (-4)(3)) + 5((-2)(5) - (-3 - \lambda)(3)) ]
- Simplify the expression
After expanding and simplifying, set the determinant equal to zero:
[ \text{det}(A - \lambda I) = 0 ]
This will yield the characteristic polynomial.
- Final characteristic equation
The final characteristic equation will be a polynomial in ( \lambda ) that can be used to find the eigenvalues.
The characteristic equation of the matrix ( A ) is:
$$ -\lambda^3 + 7\lambda^2 + 20\lambda - 18 = 0 $$
More Information
The characteristic equation is essential for finding the eigenvalues of a matrix, which are critical in various applications like stability analysis and systems of differential equations.
Tips
Common mistakes include:
- Forgetting to substitute ( -\lambda ) correctly when forming ( A - \lambda I ).
- Miscalculating the determinant by omitting signs or making arithmetic errors during expansion.
AI-generated content may contain errors. Please verify critical information