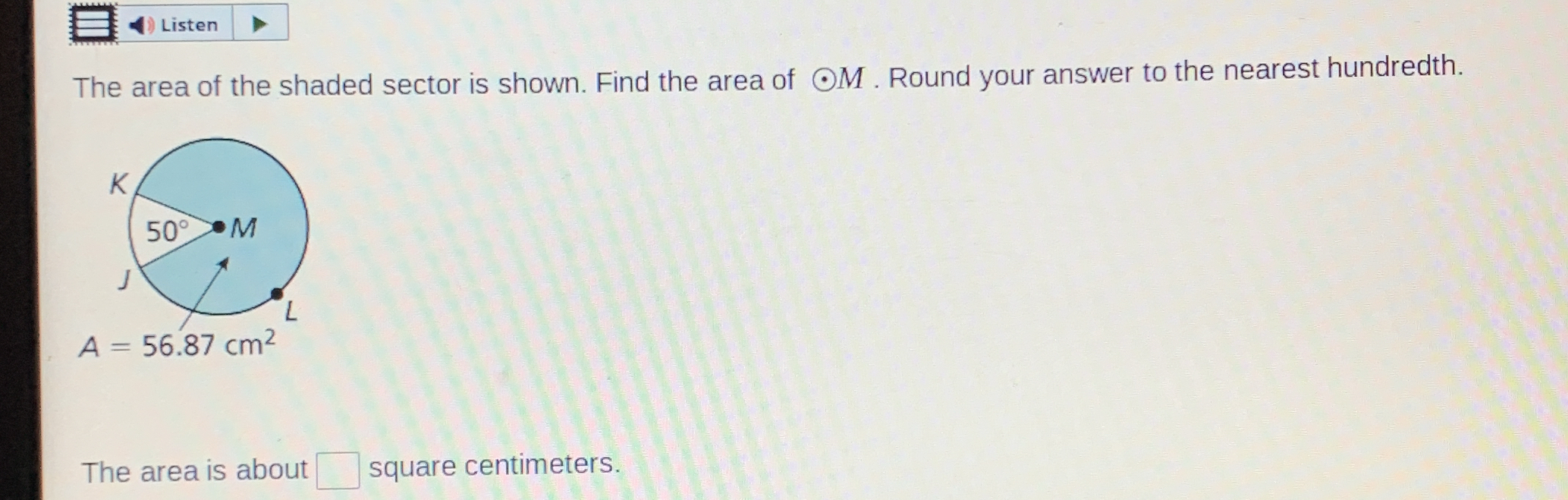
The area of the shaded sector is shown. Find the area of oM. Round your answer to the nearest hundredth.
Understand the Problem
The question asks to calculate the area of a sector in a circle, given the circumference of the entire circle. The user needs to find the area of sector OM that corresponds to a 50-degree angle, using the given area of the full circle (56.87 cm²).
Answer
$7.89 \, \text{cm}^2$
Answer for screen readers
The area of sector OM is approximately $7.89 , \text{cm}^2$.
Steps to Solve
- Identify the total area of the circle
The area of the entire circle is given as ( A = 56.87 , \text{cm}^2 ).
- Determine the fraction of the angle in radians
The full circle is ( 360^\circ ). To find the fraction of the circle represented by the sector, use the angle of the sector, which is ( 50^\circ ): [ \text{Fraction of the circle} = \frac{50^\circ}{360^\circ} ]
- Calculate the area of the sector
Multiply the area of the entire circle by the fraction of the circle: [ \text{Area of sector OM} = A \times \frac{50^\circ}{360^\circ} ] Substituting ( A = 56.87 ): [ \text{Area of sector OM} = 56.87 \times \frac{50}{360} ]
- Perform the calculation
Calculating the area: [ \text{Area of sector OM} \approx 56.87 \times 0.138888 \approx 7.89 , \text{cm}^2 ]
- Round to the nearest hundredth
The final answer, rounded to the nearest hundredth, is: [ \text{Area of sector OM} \approx 7.89 , \text{cm}^2 ]
The area of sector OM is approximately $7.89 , \text{cm}^2$.
More Information
The area of a sector can be found by using the formula for the area of the circle multiplied by the fraction of the circle that the angle represents. In this case, we calculated it based on the given area of the circle and the proportion of the angle.
Tips
- Forgetting to convert the angle into a fraction relative to ( 360^\circ ).
- Miscalculating the area of the sector by not multiplying correctly.
AI-generated content may contain errors. Please verify critical information