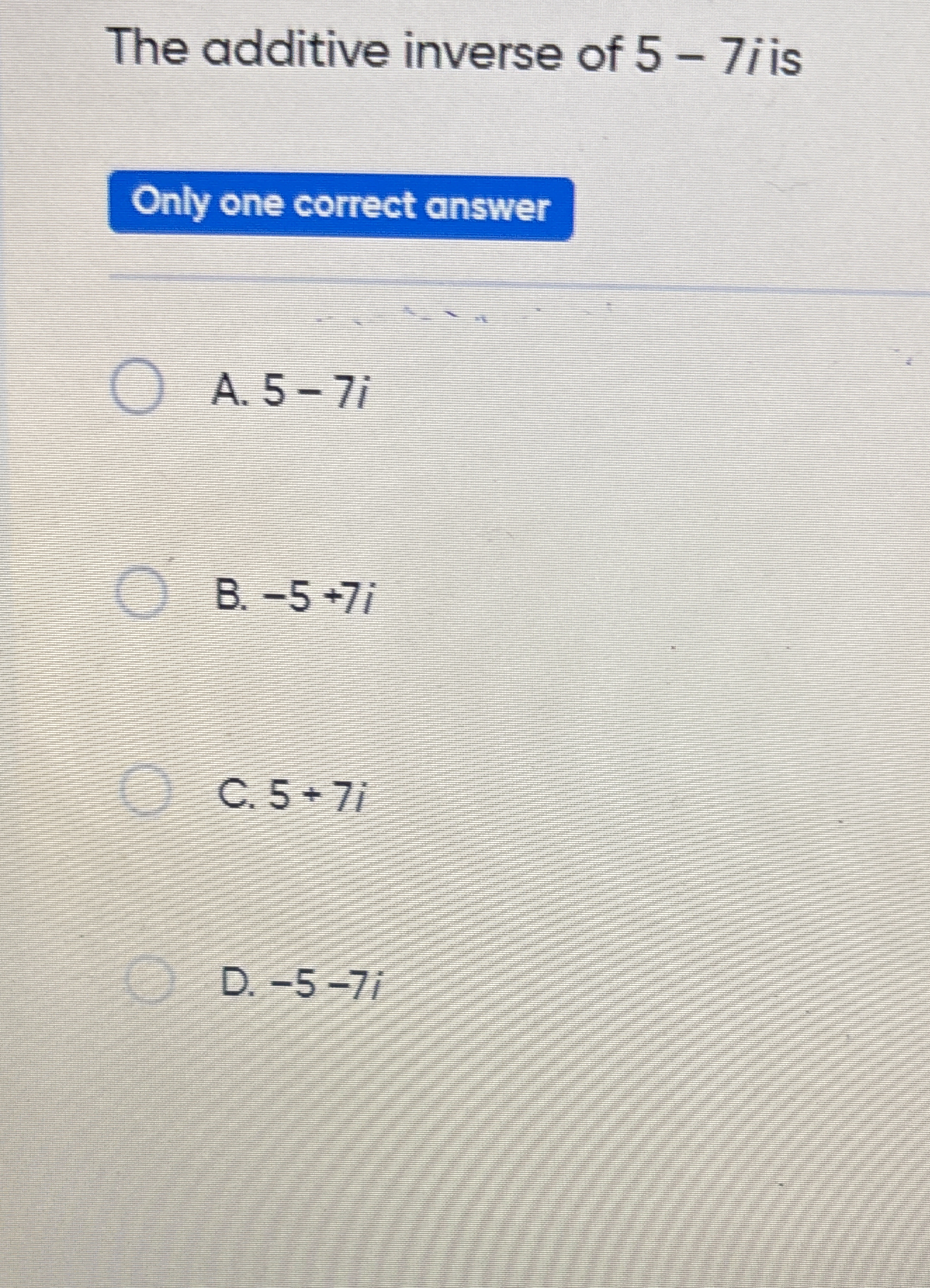
The additive inverse of 5 - 7i is
Understand the Problem
The question is asking for the additive inverse of the complex number 5 - 7i. The additive inverse of a number is what you add to it to get zero, which in this case will involve changing the signs of both the real and imaginary parts.
Answer
The additive inverse is \(-5 + 7i\).
Answer for screen readers
The additive inverse of (5 - 7i) is (-5 + 7i).
Steps to Solve
-
Identify the complex number
The given complex number is (5 - 7i). -
Change the sign of the real part
The real part is (5). The additive inverse changes its sign:
$$ -5 $$ -
Change the sign of the imaginary part
The imaginary part is (-7i). The additive inverse changes its sign:
$$ +7i $$ -
Combine the results
Combine the new real and imaginary parts to find the additive inverse:
$$ -5 + 7i $$
The additive inverse of (5 - 7i) is (-5 + 7i).
More Information
The concept of additive inverses applies to all numbers, including complex numbers. For any complex number (a + bi), its additive inverse is (-a - bi), which, when added together, results in zero.
Tips
- Forgetting to change both the real and imaginary parts when finding the additive inverse.
- Confusing the signs in the imaginary part, leading to incorrect results.
AI-generated content may contain errors. Please verify critical information