Solve z = px + qy + p^2 + q^2 by Charpit's method.
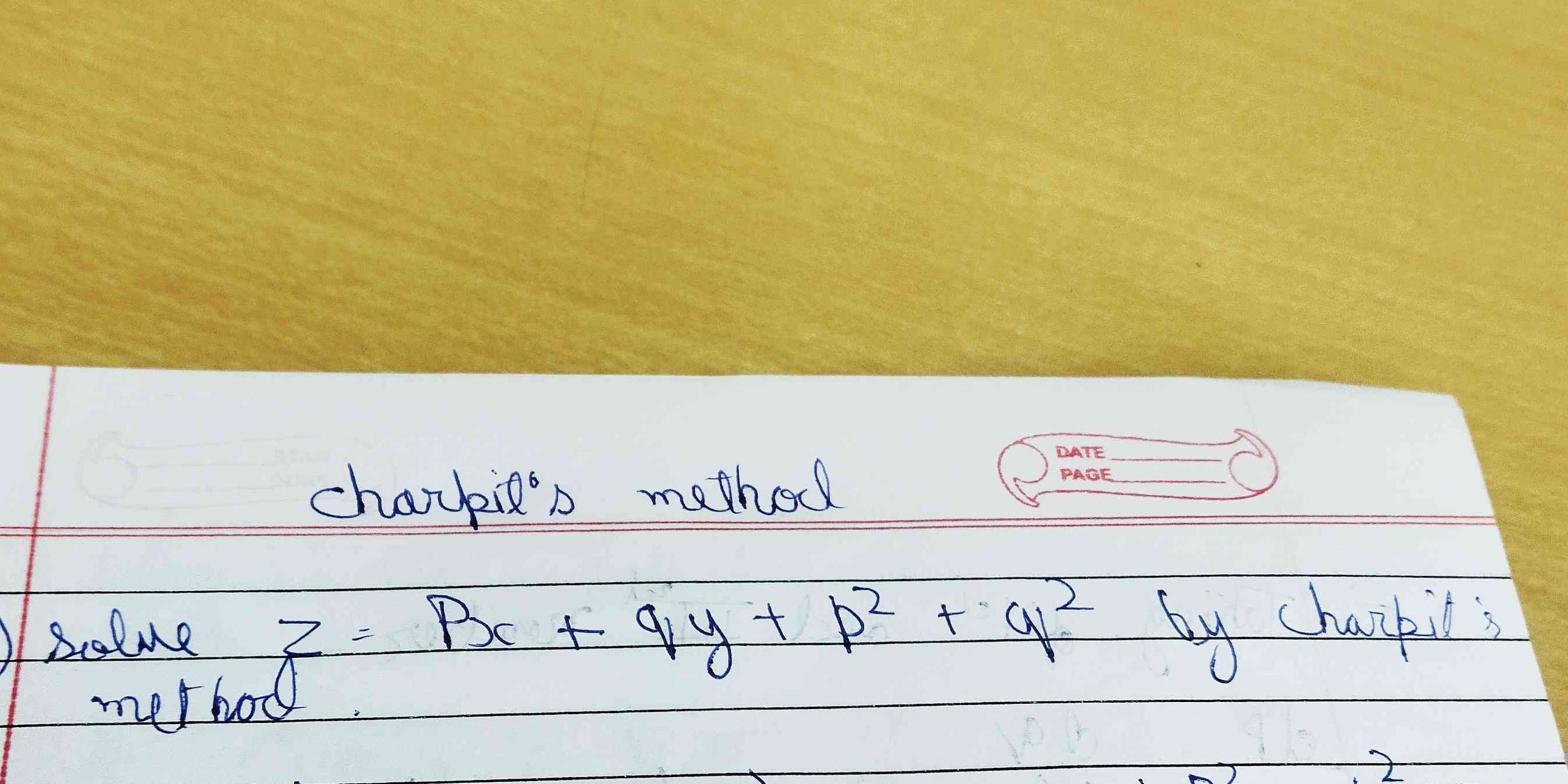
Understand the Problem
The question is asking to solve a partial differential equation (PDE) of the form z = px + qy + p^2 + q^2 using Charpit's method. This involves finding a complete integral of the given PDE by constructing and solving a system of ordinary differential equations (ODEs) derived from Charpit's equations.
Answer
$z = ax + by + a^2 + b^2$
Answer for screen readers
$z = ax + by + a^2 + b^2$
Steps to Solve
- Write the given equation and define $f$
The given equation is $z = px + qy + p^2 + q^2$
Let $f(x, y, z, p, q) = px + qy + p^2 + q^2 - z = 0$.
- Write down Charpit's equations
Charpit's equations are given by:
$$ \frac{dp}{f_x + pf_z} = \frac{dq}{f_y + qf_z} = \frac{dz}{-pf_p - qf_q} = \frac{dx}{-f_p} = \frac{dy}{-f_q} $$
- Calculate the required partial derivatives
Compute the partial derivatives of $f$ with respect to $x, y, z, p, q$:
$f_x = \frac{\partial f}{\partial x} = p$
$f_y = \frac{\partial f}{\partial y} = q$
$f_z = \frac{\partial f}{\partial z} = -1$
$f_p = \frac{\partial f}{\partial p} = x + 2p$
$f_q = \frac{\partial f}{\partial q} = y + 2q$
- Substitute the partial derivatives into Charpit's equations
Substituting these into Charpit's equations, we get:
$$ \frac{dp}{p + p(-1)} = \frac{dq}{q + q(-1)} = \frac{dz}{-p(x+2p) - q(y+2q)} = \frac{dx}{-(x+2p)} = \frac{dy}{-(y+2q)} $$
Simplifying, we have:
$$ \frac{dp}{0} = \frac{dq}{0} = \frac{dz}{-p(x+2p) - q(y+2q)} = \frac{dx}{-(x+2p)} = \frac{dy}{-(y+2q)} $$
- Choose the simplest fraction to integrate
From $\frac{dp}{0} = \frac{dq}{0}$, we have $dp = 0$ and $dq = 0$. Integrating these gives $p = a$ and $q = b$, where $a$ and $b$ are arbitrary constants.
- Substitute $p$ and $q$ into the original equation
Substitute $p = a$ and $q = b$ into the original equation $z = px + qy + p^2 + q^2$:
$z = ax + by + a^2 + b^2$
This is the complete integral.
$z = ax + by + a^2 + b^2$
More Information
The Charpit's method is a technique for finding the complete integral of a first-order partial differential equation. The complete integral contains as many arbitrary constants as there are independent variables. In this case, we have two independent variables $x$ and $y$, and the complete integral contains two arbitrary constants $a$ and $b$.
Tips
A common mistake is making errors in calculating the partial derivatives. Another common mistake is in the simplification and integration of Charpit's equations. Ensure each derivative is calculated correctly and that the simplest fractions are chosen for integration to minimize complexity.
AI-generated content may contain errors. Please verify critical information