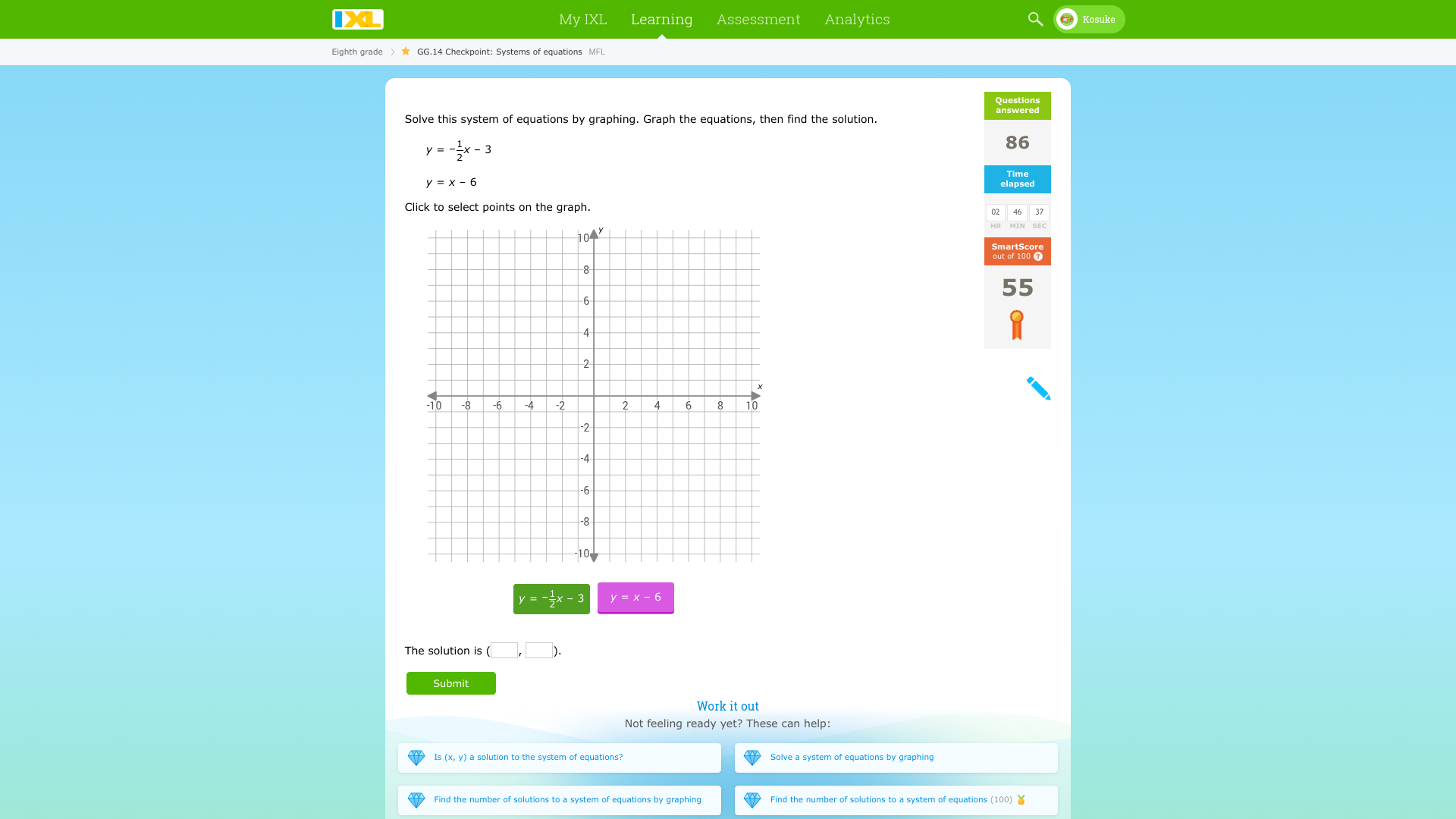
Solve this system of equations by graphing. Graph the equations, then find the solution.
Understand the Problem
The question requires us to solve a system of two equations by graphing. We need to graph the given equations, locate the intersection point to find the solution, and express it in coordinate form.
Answer
The solution is $(2, -4)$.
Answer for screen readers
The solution is $(2, -4)$.
Steps to Solve
-
Identify the equations The two equations given are: $$ y = -\frac{1}{2}x - 3 $$ $$ y = x - 6 $$
-
Convert equations into slope-intercept form Both equations are already in the slope-intercept form ($y = mx + b$), where $m$ is the slope and $b$ is the y-intercept.
-
Graph the first equation For the equation $y = -\frac{1}{2}x - 3$, plot the y-intercept at (0, -3). Use the slope of $-\frac{1}{2}$ to find another point: from (0, -3), move down 1 unit and right 2 units to reach (2, -4). Draw the line through these points.
-
Graph the second equation For the equation $y = x - 6$, plot the y-intercept at (0, -6). The slope is 1, so from (0, -6), move up 1 unit and right 1 unit to reach (1, -5). Draw the line through these points.
-
Locate the intersection point Identify where the two lines intersect on the graph. This point is the solution to the system of equations.
-
Read the coordinates From the graph, find the coordinates of the intersection point.
The solution is $(2, -4)$.
More Information
The solution $(2, -4)$ means that when $x = 2$, both equations yield $y = -4$. This point is the precise meeting point of the two lines on the graph.
Tips
- Failing to accurately plot the points can lead to incorrect intersection coordinates. Double-check the slope and the plotted points.
- Miscalculating the y-value when finding the intersection. Always verify by substituting back into both original equations.
AI-generated content may contain errors. Please verify critical information