Solve the system of equations: 4x - 2y = 31 x^2 - xy - y^2 = 1
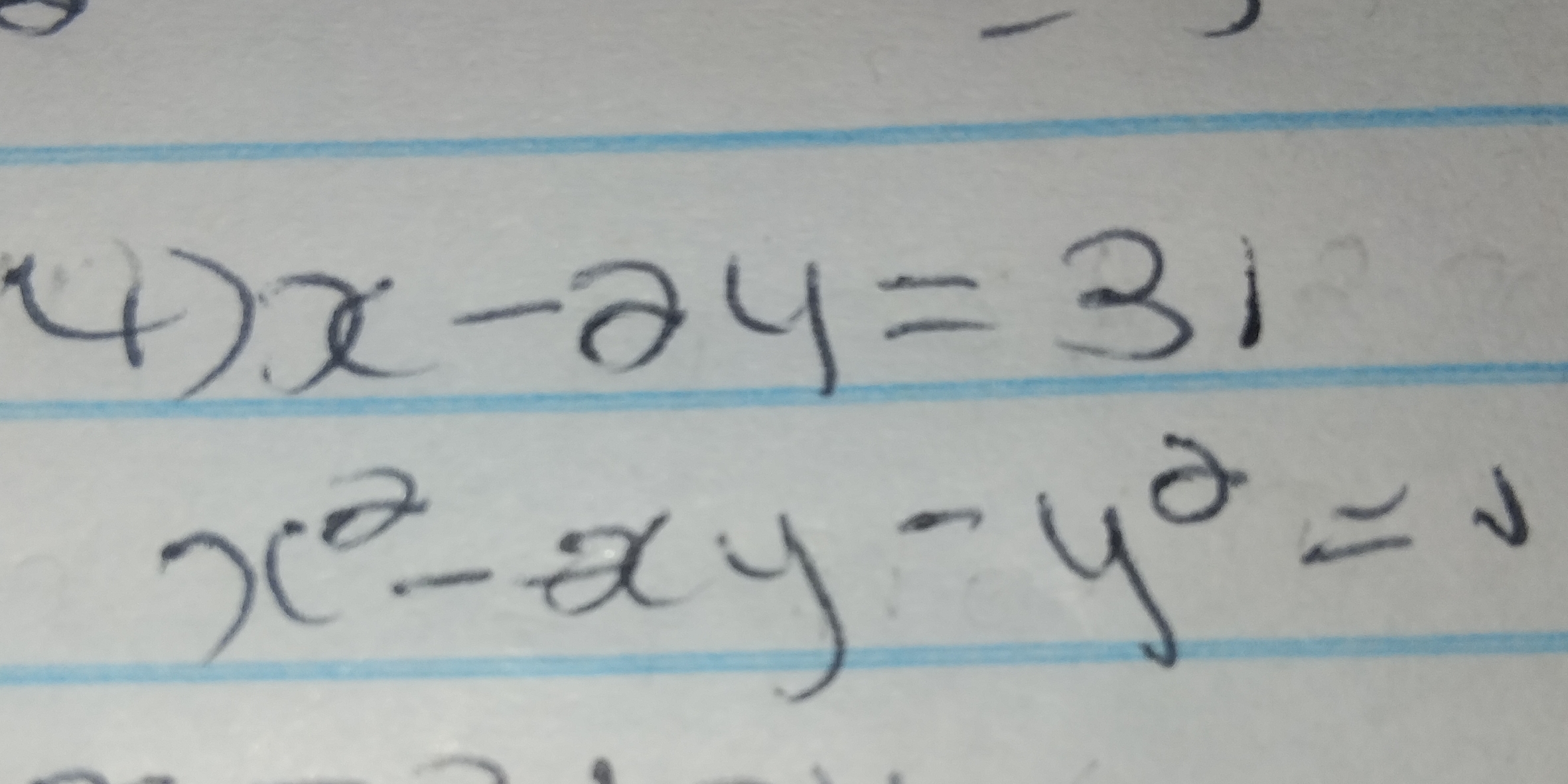
Understand the Problem
The question appears to be asking to solve a system of two equations with two variables, x and y. The equations are:
- 4x - 2y = 31
- x^2 - xy - y^2 = 1
We need to find the values of x and y that satisfy both equations simultaneously.
Answer
$x_1 = \frac{31 + 3\sqrt{21}}{4}, y_1 = \frac{3\sqrt{21}}{2}$ $x_2 = \frac{31 - 3\sqrt{21}}{4}, y_2 = -\frac{3\sqrt{21}}{2}$
Answer for screen readers
The solutions to the system of equations are:
$x_1 = \frac{31 + 3\sqrt{21}}{4}, \quad y_1 = \frac{3\sqrt{21}}{2}$
$x_2 = \frac{31 - 3\sqrt{21}}{4}, \quad y_2 = -\frac{3\sqrt{21}}{2}$
Steps to Solve
-
Solve the first equation for y We'll isolate $y$ in the equation $4x - 2y = 31$. $$ 4x - 2y = 31 $$ Subtract $4x$ from both sides: $$ -2y = 31 - 4x $$ Divide both sides by $-2$: $$ y = \frac{4x - 31}{2} $$
-
Substitute y into the second equation Now, replace $y$ in the second equation $x^2 - xy - y^2 = 1$ with $\frac{4x - 31}{2}$: $$ x^2 - x\left(\frac{4x - 31}{2}\right) - \left(\frac{4x - 31}{2}\right)^2 = 1 $$
-
Simplify the second equation Let's simplify the equation: $$ x^2 - \frac{4x^2 - 31x}{2} - \frac{(4x - 31)^2}{4} = 1 $$ Expand $(4x - 31)^2$: $$ (4x - 31)^2 = 16x^2 - 248x + 961 $$ Substitute it back into the equation: $$ x^2 - \frac{4x^2 - 31x}{2} - \frac{16x^2 - 248x + 961}{4} = 1 $$ Multiply the entire equation by 4 to eliminate the fractions: $$ 4x^2 - 2(4x^2 - 31x) - (16x^2 - 248x + 961) = 4 $$ $$ 4x^2 - 8x^2 + 62x - 16x^2 + 248x - 961 = 4 $$ Combine like terms: $$ -20x^2 + 310x - 961 = 4 $$ Move the constant to the left side: $$ -20x^2 + 310x - 965 = 0 $$ Multiply by -1 to simplify: $$ 20x^2 - 310x + 965 = 0 $$ Divide by 5 to further simplify: $$ 4x^2 - 62x + 193 = 0 $$
-
Solve the quadratic equation for x We can use the quadratic formula to solve for $x$: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ Where $a = 4$, $b = -62$, and $c = 193$. $$ x = \frac{62 \pm \sqrt{(-62)^2 - 4(4)(193)}}{2(4)} $$ $$ x = \frac{62 \pm \sqrt{3844 - 3088}}{8} $$ $$ x = \frac{62 \pm \sqrt{756}}{8} $$ $$ x = \frac{62 \pm 6\sqrt{21}}{8} $$ $$ x = \frac{31 \pm 3\sqrt{21}}{4} $$ So, $x_1 = \frac{31 + 3\sqrt{21}}{4}$ and $x_2 = \frac{31 - 3\sqrt{21}}{4}$
-
Solve for y Substitute $x_1$ and $x_2$ into the equation $y = \frac{4x - 31}{2}$ to find the corresponding $y$ values. For $x_1 = \frac{31 + 3\sqrt{21}}{4}$: $$ y_1 = \frac{4\left(\frac{31 + 3\sqrt{21}}{4}\right) - 31}{2} = \frac{31 + 3\sqrt{21} - 31}{2} = \frac{3\sqrt{21}}{2} $$ For $x_2 = \frac{31 - 3\sqrt{21}}{4}$: $$ y_2 = \frac{4\left(\frac{31 - 3\sqrt{21}}{4}\right) - 31}{2} = \frac{31 - 3\sqrt{21} - 31}{2} = \frac{-3\sqrt{21}}{2} $$
-
The solutions The solutions are: $$ x_1 = \frac{31 + 3\sqrt{21}}{4}, \quad y_1 = \frac{3\sqrt{21}}{2} $$ $$ x_2 = \frac{31 - 3\sqrt{21}}{4}, \quad y_2 = -\frac{3\sqrt{21}}{2} $$
The solutions to the system of equations are:
$x_1 = \frac{31 + 3\sqrt{21}}{4}, \quad y_1 = \frac{3\sqrt{21}}{2}$
$x_2 = \frac{31 - 3\sqrt{21}}{4}, \quad y_2 = -\frac{3\sqrt{21}}{2}$
More Information
These are the values of $x$ and $y$ that simultaneously satisfy the equations $4x - 2y = 31$ and $x^2 - xy - y^2 = 1$.
Tips
- Algebraic errors: Mistakes can be easily made when simplifying and expanding expressions, especially when dealing with fractions and square roots. Careful attention to detail is crucial.
- Incorrectly applying the quadratic formula: Ensure correct identification of $a$, $b$, and $c$ and correct substitution into the formula.
- Forgetting to solve for y: After finding the x values, it's important to substitute them back into one of the original equations to find the corresponding y values.
- Not simplifying the quadratic equation: Can lead to using larger numbers in the quadratic equation, making it more prone to error
AI-generated content may contain errors. Please verify critical information