Solve the integral of x * e^(x^2 - 1) dx
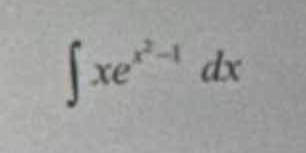
Understand the Problem
The question requires us to evaluate the given indefinite integral. We need to find the antiderivative of the function x * e^(x^2 - 1) with respect to x. We will use u-substitution to solve this problem.
Answer
$\frac{1}{2}e^{x^2-1} + C$
Answer for screen readers
$\frac{1}{2}e^{x^2-1} + C$
Steps to Solve
- Perform u-substitution
Let $u = x^2 - 1$. Then, we need to find $du$. Taking the derivative of $u$ with respect to $x$, we have: $$ \frac{du}{dx} = 2x $$ Therefore $du = 2x , dx$.
- Rewrite the integral to incorporate the u-substitution
We have $x,dx$ in our integral, but we have $2x,dx$ in our expression for $du$. So, we rewrite the equation such that $$x,dx = \frac{1}{2} du$$ Now, we can rewrite the integral in terms of $u$: $$ \int xe^{x^2-1} dx = \int e^u \cdot \frac{1}{2} du = \frac{1}{2} \int e^u du $$
- Integrate with respect to u
The antiderivative of $e^u$ with respect to $u$ is simply $e^u$. So, we have: $$ \frac{1}{2} \int e^u du = \frac{1}{2} e^u + C $$
- Substitute back for x
Now we substitute $x^2 - 1$ back in for $u$: $$ \frac{1}{2} e^u + C = \frac{1}{2} e^{x^2 - 1} + C $$
$\frac{1}{2}e^{x^2-1} + C$
More Information
The indefinite integral of $ xe^{x^2-1} $ is $ \frac{1}{2}e^{x^2-1} + C $, where $ C $ is the constant of integration.
Tips
A common mistake is forgetting to include the constant of integration, $C$, when evaluating indefinite integrals. Another common mistake is not correctly solving for $dx$ in terms of $du$, or not substituting correctly back into the original variable.
AI-generated content may contain errors. Please verify critical information