Solve the following systems of equations: b. 2 * (3x - y/2) = 1/4; 7 + (1/2)y = 3x c. (x + y)/3 + (2x)/5 = 1/3; (4x)/5 - 3 * (x - 2y)/2 = 3 d. 2x - 3y = 13; (5x - 1)/3 = (y - 3)/... Solve the following systems of equations: b. 2 * (3x - y/2) = 1/4; 7 + (1/2)y = 3x c. (x + y)/3 + (2x)/5 = 1/3; (4x)/5 - 3 * (x - 2y)/2 = 3 d. 2x - 3y = 13; (5x - 1)/3 = (y - 3)/4

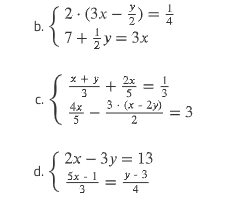
Question image

Understand the Problem

The problem presents three systems of linear equations (b, c, d) and requires solving each system to find the values of x and y that satisfy both equations in each system. This is a classic algebra problem, where we will likely need to use methods like substitution or elimination to find the solutions for (x) and (y).

Answer

b. No solution c. $x = 0$, $y = 1$ d. $x = -1$, $y = -5$
Answer for screen readers

b. No solution c. $x = 0$, $y = 1$ d. $x = -1$, $y = -5$

Steps to Solve

b. $\begin{cases} 2 \cdot (3x - \frac{y}{2}) = \frac{1}{4} \ 7 + \frac{1}{2} y = 3x \end{cases}$

  1. Simplify the first equation Distribute the 2 in the first equation: $2 \cdot (3x - \frac{y}{2}) = 6x - y = \frac{1}{4}$

  2. Solve the second equation for $y$ Isolate $y$ in the second equation: $\frac{1}{2} y = 3x - 7$ $y = 6x - 14$

  3. Substitution Substitute the expression for $y$ from step 2 into the simplified first equation from step 1: $6x - (6x - 14) = \frac{1}{4}$ $6x - 6x + 14 = \frac{1}{4}$ $14 = \frac{1}{4}$ Since $14 = \frac{1}{4}$ is false, there is no solution for this system of equations

c. $\begin{cases} \frac{x + y}{3} + \frac{2x}{5} = \frac{1}{3} \ \frac{4x}{5} - \frac{3 \cdot (x - 2y)}{2} = 3 \end{cases}$

  1. Clear fractions in the first equation Multiply both sides of the first equation by 15: $15 \cdot (\frac{x + y}{3} + \frac{2x}{5}) = 15 \cdot \frac{1}{3}$ $5(x + y) + 6x = 5$ $5x + 5y + 6x = 5$ $11x + 5y = 5$

  2. Clear fractions in the second equation Multiply both sides of the second equation by 10: $10 \cdot (\frac{4x}{5} - \frac{3 \cdot (x - 2y)}{2}) = 10 \cdot 3$ $8x - 15(x - 2y) = 30$ $8x - 15x + 30y = 30$ $-7x + 30y = 30$

  3. Solve for $x$ in the first equation $11x = 5 - 5y$ $x = \frac{5 - 5y}{11}$

  4. Substitution Substitute the expression for $x$ from step 3 into the second equation: $-7(\frac{5 - 5y}{11}) + 30y = 30$ Multiply both sides by 11: $-7(5 - 5y) + 330y = 330$ $-35 + 35y + 330y = 330$ $365y = 365$ $y = 1$

  5. Solve for $x$ Substitute $y = 1$ into the expression for $x$: $x = \frac{5 - 5(1)}{11} = \frac{5 - 5}{11} = \frac{0}{11} = 0$

d. $\begin{cases} 2x - 3y = 13 \ \frac{5x - 1}{3} = \frac{y - 3}{4} \end{cases}$

  1. Clear fractions in the second equation Multiply both sides of the second equation by 12: $12 \cdot (\frac{5x - 1}{3}) = 12 \cdot (\frac{y - 3}{4})$ $4(5x - 1) = 3(y - 3)$ $20x - 4 = 3y - 9$ $20x - 3y = -5$

  2. Solve for $y$ in the first equation $-3y = 13 - 2x$ $3y = 2x - 13$ $y = \frac{2x - 13}{3}$

  3. Substitution Substitute the expression for $y$ from step 2 into the modified second equation from step 1: $20x - 3(\frac{2x - 13}{3}) = -5$ $20x - (2x - 13) = -5$ $20x - 2x + 13 = -5$ $18x = -18$ $x = -1$

  4. Solve for $y$ Substitute $x = -1$ into the expression for $y$: $y = \frac{2(-1) - 13}{3} = \frac{-2 - 13}{3} = \frac{-15}{3} = -5$

b. No solution c. $x = 0$, $y = 1$ d. $x = -1$, $y = -5$

More Information

When solving systems of linear equations, it's important to check whether a solution exists. In system 'b', we found that the equations were contradictory, so there was no solution. Systems 'c' and 'd' had unique solutions found using substitution and elimination techniques.

Tips

  • Forgetting to distribute when clearing parentheses
  • Making arithmetic errors when multiplying or dividing to isolate variables
  • Incorrectly substituting values into equations
  • Not checking the solution by plugging the values of $x$ and $y$ back into the original equations

AI-generated content may contain errors. Please verify critical information

Thank you for voting!
Use Quizgecko on...
Browser
Open
Browser
Browser