Solve the following system of equations: 2x + 3y = 13 7x - 5y = -1
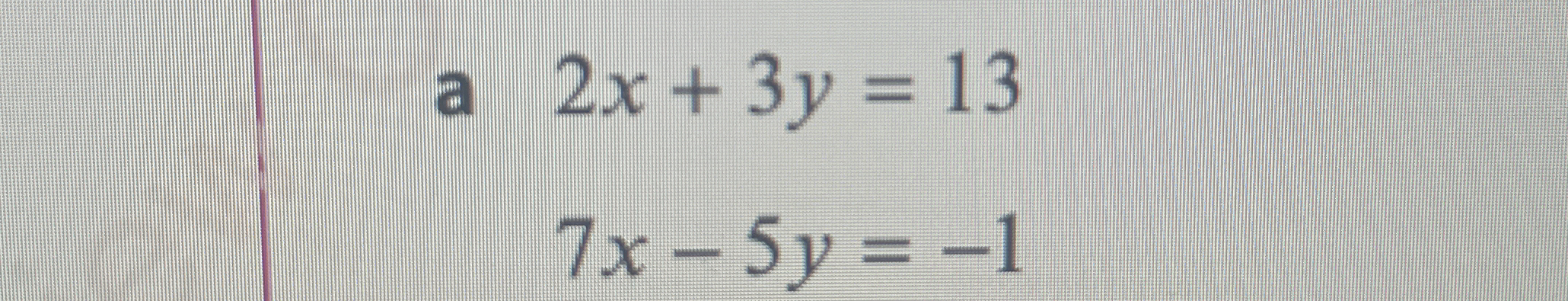
Understand the Problem
The question asks to solve the system of equations:
2x + 3y = 13 7x - 5y = -1
We need to find the values of x and y that satisfy both equations.
Answer
$x = 2$, $y = 3$
Answer for screen readers
$x=2$, $y=3$
Steps to Solve
-
Choose a variable to eliminate We can choose to eliminate either $x$ or $y$. Let's eliminate $y$.
-
Multiply the equations by appropriate constants Multiply the first equation by $5$ and the second equation by $3$ to make the coefficients of $y$ opposites. $$5(2x + 3y) = 5(13)$$ $$3(7x - 5y) = 3(-1)$$ This gives us: $$10x + 15y = 65$$ $$21x - 15y = -3$$
-
Add the equations together Add the two equations to eliminate $y$: $$(10x + 15y) + (21x - 15y) = 65 + (-3)$$ $$31x = 62$$
-
Solve for $x$ Divide both sides by $31$: $$x = \frac{62}{31}$$ $$x = 2$$
-
Substitute $x$ into one of the original equations Substitute $x = 2$ into the first original equation: $$2(2) + 3y = 13$$ $$4 + 3y = 13$$
-
Solve for $y$ Subtract $4$ from both sides: $$3y = 9$$ Divide both sides by $3$: $$y = \frac{9}{3}$$ $$y = 3$$
$x=2$, $y=3$
More Information
The solution to the system of equations is $x = 2$ and $y = 3$. This means that the point $(2, 3)$ is the intersection of the two lines represented by the equations.
Tips
A common mistake is to make an error when multiplying the equations by a constant. Make sure to distribute the constant to every term in the equation. Another common mistake is to add the equations incorrectly, especially when dealing with negative signs.
AI-generated content may contain errors. Please verify critical information