Solve the following problems: 1. Find the secant line that joins the points on the graph of f(x) = 5x^2 - 8x. 2. Find the rate of change as x changes from -1 to 4 for f(x) = 5x^2... Solve the following problems: 1. Find the secant line that joins the points on the graph of f(x) = 5x^2 - 8x. 2. Find the rate of change as x changes from -1 to 4 for f(x) = 5x^2 - 8x. 3. Find the line that is tangent to the graph of the function f(x) = 5x^2 - 8x. 4. Determine if h(x) = 2 / sqrt(x+5) is tangent to f(x) at the point P(4, 2/3). 5. Determine if f(x) = 5 / (x-2) is tangent to f(x) at the point P(4, 5/2). 6. Analyze the piecewise function f(x) = { 4-x^2, if x <= 1; 2x+1, if x > 1 } at each of the...
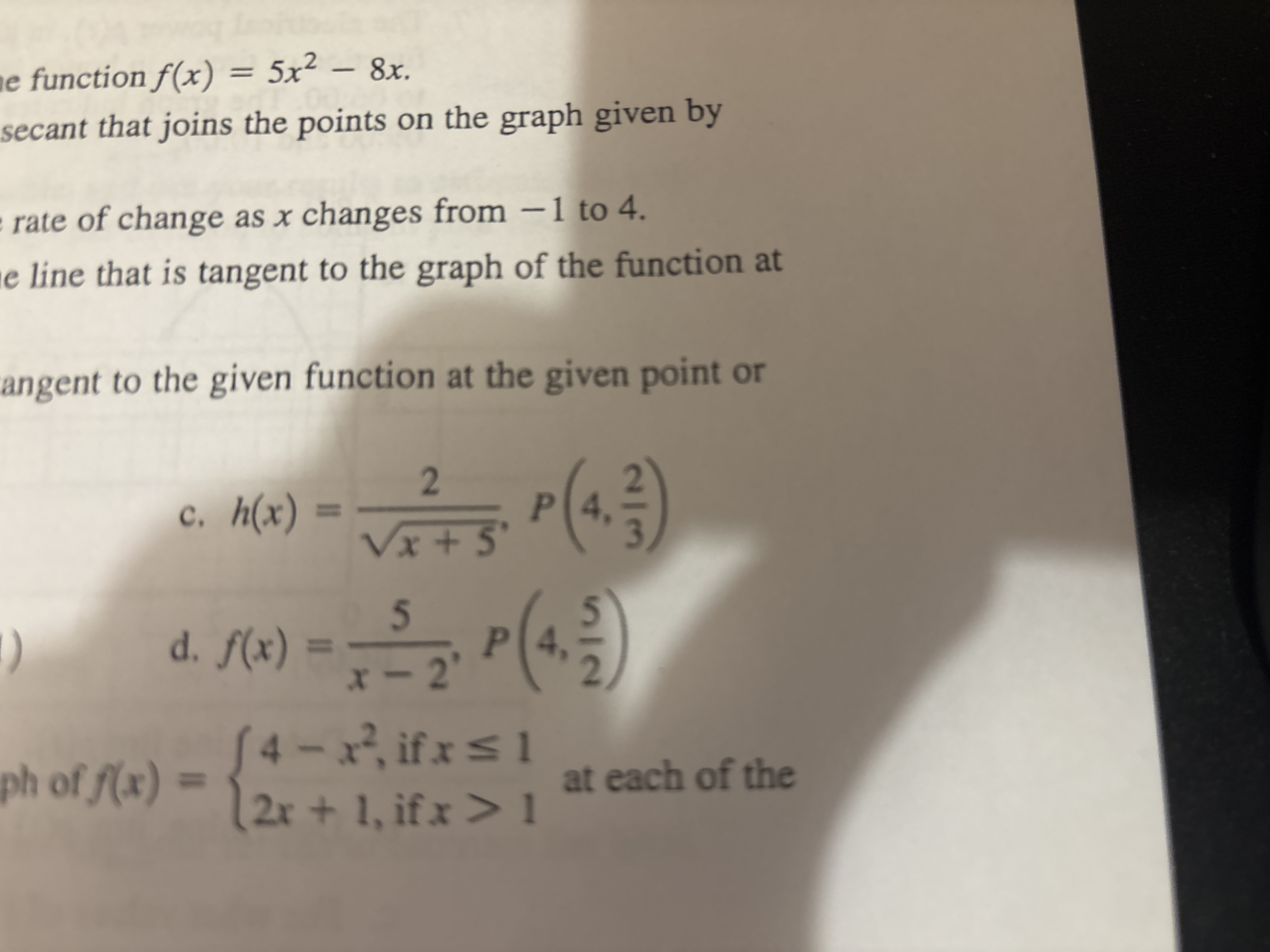
Understand the Problem
The image contains several math problems related to functions and calculus. Specifically, it references finding the secant line, the rate of change of a function over an interval, the tangent line to a graph, and determining tangency to a function at a point. There are two particular function examples given with points, and a piecewise function.
Answer
$y = 7x + 20$
Answer for screen readers
The equation of the secant line is $ y = 7x + 20 $.
Steps to Solve
- Find the y-coordinates of the given x-values
To find the secant line, we first need the points on the function $ f(x) = 5x^2 - 8x $ at $ x = -1 $ and $ x = 4 $. Calculate $ f(-1) $: $ f(-1) = 5(-1)^2 - 8(-1) = 5(1) + 8 = 5 + 8 = 13 $ So, the first point is $ (-1, 13) $. Calculate $ f(4) $: $ f(4) = 5(4)^2 - 8(4) = 5(16) - 32 = 80 - 32 = 48 $ So, the second point is $ (4, 48) $.
- Calculate the slope of the secant line
The slope of the secant line, $ m $, is given by the formula: $ m = \frac{y_2 - y_1}{x_2 - x_1} $ Using the points $ (-1, 13) $ and $ (4, 48) $: $ m = \frac{48 - 13}{4 - (-1)} = \frac{35}{5} = 7 $
- Find the equation of the secant line
Using the point-slope form of a line, $ y - y_1 = m(x - x_1) $, and the point $ (-1, 13) $, we can write the equation of the secant line: $ y - 13 = 7(x - (-1)) $ $ y - 13 = 7(x + 1) $ $ y - 13 = 7x + 7 $ $ y = 7x + 20 $
The equation of the secant line is $ y = 7x + 20 $.
More Information
The secant line represents the average rate of change of the function $f(x)$ over the interval $[-1, 4]$.
Tips
A common mistake is to incorrectly calculate the y-coordinates or to use the wrong formula for the slope. Another common mistake is to incorrectly simplify the equation of the line.
AI-generated content may contain errors. Please verify critical information