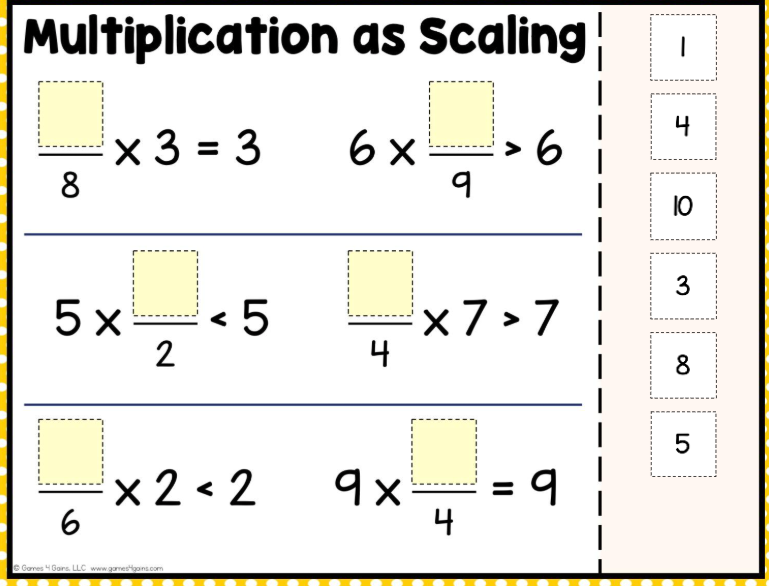
Solve the following multiplication scaling problems by filling in the blanks with the appropriate numbers.
Understand the Problem
The problem presents a series of incomplete multiplication equations where a missing number needs to be determined. The goal is to identify the number from the provided list (1, 4, 10, 3, 8, 5) that, when placed in the blank, satisfies each equation or inequality. The equations involve both whole numbers and fractions, requiring an understanding of multiplication and inequalities.
Answer
$\frac{8}{8}$ x 3 = 3 6 x $\frac{10}{9}$ > 6 5 x $\frac{1}{2}$ < 5 $\frac{5}{4}$ x 7 > 7 $\frac{3}{6}$ x 2 < 2 9 x $\frac{4}{4}$ = 9
Answer for screen readers
$\frac{8}{8}$ x 3 = 3
6 x $\frac{10}{9}$ > 6
5 x $\frac{1}{2}$ < 5
$\frac{5}{4}$ x 7 > 7
$\frac{3}{6}$ x 2 < 2
9 x $\frac{4}{4}$ = 9
Steps to Solve
- Solve the first equation: $\frac{\square}{8} \times 3 = 3$
To solve $\frac{\square}{8} \times 3 = 3$, we need to isolate the fraction. Divide both sides of the equation by 3:
$\frac{\square}{8} = \frac{3}{3}$ $\frac{\square}{8} = 1$
Multiply both sides by 8 to find the missing number:
$\square = 1 \times 8$ $\square = 8$
- Solve the second inequality: $6 \times \frac{\square}{9} > 6$
To solve $6 \times \frac{\square}{9} > 6$, divide both sides by 6:
$\frac{\square}{9} > \frac{6}{6}$ $\frac{\square}{9} > 1$
Multiply both sides by 9:
$\square > 1 \times 9$ $\square > 9$
From the given list (1, 4, 10, 3, 8, 5), the number that satisfies $\square > 9$ is 10.
- Solve the third inequality: $5 \times \frac{\square}{2} < 5$
To solve $5 \times \frac{\square}{2} < 5$, divide both sides by 5:
$\frac{\square}{2} < \frac{5}{5}$ $\frac{\square}{2} < 1$
Multiply both sides by 2:
$\square < 1 \times 2$ $\square < 2$
From the given list (1, 4, 10, 3, 8, 5), the number that satisfies $\square < 2$ is 1.
- Solve the fourth inequality: $\frac{\square}{4} \times 7 > 7$
To solve $\frac{\square}{4} \times 7 > 7$, divide both sides by 7:
$\frac{\square}{4} > \frac{7}{7}$ $\frac{\square}{4} > 1$
Multiply both sides by 4:
$\square > 1 \times 4$ $\square > 4$
From the given list (1, 4, 10, 3, 8, 5), the numbers that satisfy $\square > 4$ are 5, 8 and 10, but 8 and 10 has been used already. 5 is our only value 5. Solve the fifth inequality: $\frac{\square}{6} \times 2 < 2$
To solve $\frac{\square}{6} \times 2 < 2$, divide both sides by 2:
$\frac{\square}{6} < \frac{2}{2}$ $\frac{\square}{6} < 1$
Multiply both sides by 6:
$\square < 1 \times 6$ $\square < 6$
From the given list (1, 4, 10, 3, 8, 5), the numbers that satisfy $\square < 6$ are 3 and 4 3 is our only value
- Solve the sixth equation: $9 \times \frac{\square}{4} = 9$
To solve $9 \times \frac{\square}{4} = 9$, divide both sides by 9:
$\frac{\square}{4} = \frac{9}{9}$ $\frac{\square}{4} = 1$
Multiply both sides by 4:
$\square = 1 \times 4$ $\square = 4$
$\frac{8}{8}$ x 3 = 3
6 x $\frac{10}{9}$ > 6
5 x $\frac{1}{2}$ < 5
$\frac{5}{4}$ x 7 > 7
$\frac{3}{6}$ x 2 < 2
9 x $\frac{4}{4}$ = 9
More Information
The problem demonstrates how multiplication by a fraction can scale a number up, down, or leave it unchanged, depending on whether the fraction is greater than, less than, or equal to 1.
Tips
A common mistake is not isolating the fraction correctly before determining the missing number, which can lead to incorrect inequality or equality evaluations. Additionally, one might forget to check whether the chosen numbers have already been used.
AI-generated content may contain errors. Please verify critical information