Solve the following limit problems: 1. $\lim_{x \to +\infty} \frac{5x-4}{2x+3}$ 2. $\lim_{x \to +\infty} \frac{x-2}{x^2-3}$ 3. $\lim_{x \to +\infty} \frac{4x-3}{\sqrt{3x^2-2}}$... Solve the following limit problems: 1. $\lim_{x \to +\infty} \frac{5x-4}{2x+3}$ 2. $\lim_{x \to +\infty} \frac{x-2}{x^2-3}$ 3. $\lim_{x \to +\infty} \frac{4x-3}{\sqrt{3x^2-2}}$ 4. $\lim_{x \to -\infty} \frac{\sqrt{7+4x^2}}{2x+5}$ 5. $\lim_{x \to -\infty} \frac{x^2}{x+5}$ 6. $\lim_{x \to +\infty} \frac{4x^2+x^6}{1-5x^3}$ 7. $\lim_{x \to +\infty} (3x^4-15x^3-9)$ 8. $\lim_{x \to +\infty} (3x^3-12x^2-10x-15)$

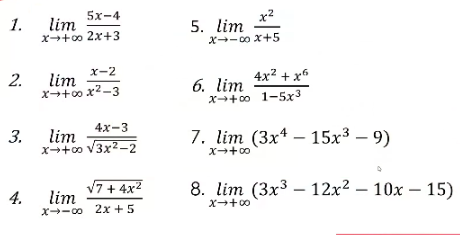
Question image

Understand the Problem

The image contains a set of calculus problems involving limits. Each problem requires evaluating the limit of a given function as x approaches infinity or negative infinity. The functions include rational functions, polynomials, and expressions involving square roots. The question is asking for step-by-step solutions to each of these limit problems.

Answer

1. $\frac{5}{2}$ 2. $0$ 3. $\frac{4\sqrt{3}}{3}$ 4. $-1$ 5. $-\infty$ 6. $-\infty$ 7. $\infty$ 8. $\infty$
Answer for screen readers
  1. $\frac{5}{2}$
  2. $0$
  3. $\frac{4\sqrt{3}}{3}$
  4. $-1$
  5. $-\infty$
  6. $-\infty$
  7. $\infty$
  8. $\infty$

Steps to Solve

  1. Evaluate $\lim_{x \to +\infty} \frac{5x-4}{2x+3}$

Divide both the numerator and denominator by the highest power of $x$ in the denominator, which is $x$.

$$ \lim_{x \to +\infty} \frac{5x-4}{2x+3} = \lim_{x \to +\infty} \frac{\frac{5x}{x}-\frac{4}{x}}{\frac{2x}{x}+\frac{3}{x}} = \lim_{x \to +\infty} \frac{5-\frac{4}{x}}{2+\frac{3}{x}} $$

As $x$ approaches infinity, $\frac{4}{x}$ and $\frac{3}{x}$ approach 0.

$$ \lim_{x \to +\infty} \frac{5-\frac{4}{x}}{2+\frac{3}{x}} = \frac{5-0}{2+0} = \frac{5}{2} $$

  1. Evaluate $\lim_{x \to +\infty} \frac{x-2}{x^2-3}$

Divide both the numerator and denominator by the highest power of $x$ in the denominator, which is $x^2$.

$$ \lim_{x \to +\infty} \frac{x-2}{x^2-3} = \lim_{x \to +\infty} \frac{\frac{x}{x^2}-\frac{2}{x^2}}{\frac{x^2}{x^2}-\frac{3}{x^2}} = \lim_{x \to +\infty} \frac{\frac{1}{x}-\frac{2}{x^2}}{1-\frac{3}{x^2}} $$

As $x$ approaches infinity, $\frac{1}{x}$, $\frac{2}{x^2}$, and $\frac{3}{x^2}$ approach 0.

$$ \lim_{x \to +\infty} \frac{\frac{1}{x}-\frac{2}{x^2}}{1-\frac{3}{x^2}} = \frac{0-0}{1-0} = \frac{0}{1} = 0 $$

  1. Evaluate $\lim_{x \to +\infty} \frac{4x-3}{\sqrt{3x^2-2}}$

Divide both the numerator and denominator by $x$. Note that dividing $\sqrt{3x^2 - 2}$ by $x$ is the same as dividing by $\sqrt{x^2}$ and placing under the square root.

$$ \lim_{x \to +\infty} \frac{4x-3}{\sqrt{3x^2-2}} = \lim_{x \to +\infty} \frac{\frac{4x}{x}-\frac{3}{x}}{\sqrt{\frac{3x^2}{x^2}-\frac{2}{x^2}}} = \lim_{x \to +\infty} \frac{4-\frac{3}{x}}{\sqrt{3-\frac{2}{x^2}}} $$

As $x$ approaches infinity, $\frac{3}{x}$ and $\frac{2}{x^2}$ approach 0.

$$ \lim_{x \to +\infty} \frac{4-\frac{3}{x}}{\sqrt{3-\frac{2}{x^2}}} = \frac{4-0}{\sqrt{3-0}} = \frac{4}{\sqrt{3}} = \frac{4\sqrt{3}}{3} $$

  1. Evaluate $\lim_{x \to -\infty} \frac{\sqrt{7+4x^2}}{2x+5}$

Divide both the numerator and denominator by $x$. Since $x$ approaches $-\infty$, $x = -\sqrt{x^2}$.

$$ \lim_{x \to -\infty} \frac{\sqrt{7+4x^2}}{2x+5} = \lim_{x \to -\infty} \frac{\frac{\sqrt{7+4x^2}}{-\sqrt{x^2}}}{\frac{2x}{x}+\frac{5}{x}} = \lim_{x \to -\infty} \frac{-\sqrt{\frac{7}{x^2}+\frac{4x^2}{x^2}}}{2+\frac{5}{x}} = \lim_{x \to -\infty} \frac{-\sqrt{\frac{7}{x^2}+4}}{2+\frac{5}{x}} $$

As $x$ approaches negative infinity, $\frac{7}{x^2}$ and $\frac{5}{x}$ approach 0.

$$ \lim_{x \to -\infty} \frac{-\sqrt{\frac{7}{x^2}+4}}{2+\frac{5}{x}} = \frac{-\sqrt{0+4}}{2+0} = \frac{-2}{2} = -1 $$

  1. Evaluate $\lim_{x \to -\infty} \frac{x^2}{x+5}$

Divide both the numerator and denominator by the highest power of $x$ in the denominator, which is $x$.

$$ \lim_{x \to -\infty} \frac{x^2}{x+5} = \lim_{x \to -\infty} \frac{\frac{x^2}{x}}{\frac{x}{x}+\frac{5}{x}} = \lim_{x \to -\infty} \frac{x}{1+\frac{5}{x}} $$

As $x$ approaches negative infinity, $\frac{5}{x}$ approaches 0.

$$ \lim_{x \to -\infty} \frac{x}{1+\frac{5}{x}} = \frac{-\infty}{1+0} = -\infty $$

  1. Evaluate $\lim_{x \to +\infty} \frac{4x^2+x^6}{1-5x^3}$

Divide both the numerator and denominator by the highest power of $x$ in the denominator, which is $x^3$.

$$ \lim_{x \to +\infty} \frac{4x^2+x^6}{1-5x^3} = \lim_{x \to +\infty} \frac{\frac{4x^2}{x^3}+\frac{x^6}{x^3}}{\frac{1}{x^3}-\frac{5x^3}{x^3}} = \lim_{x \to +\infty} \frac{\frac{4}{x}+x^3}{\frac{1}{x^3}-5} $$

As $x$ approaches infinity, $\frac{4}{x}$ and $\frac{1}{x^3}$ approach 0.

$$ \lim_{x \to +\infty} \frac{\frac{4}{x}+x^3}{\frac{1}{x^3}-5} = \frac{0+\infty}{0-5} = \frac{\infty}{-5} = -\infty $$

  1. Evaluate $\lim_{x \to +\infty} (3x^4-15x^3-9)$

Factor out the highest power of $x$, which is $x^4$.

$$ \lim_{x \to +\infty} (3x^4-15x^3-9) = \lim_{x \to +\infty} x^4(3-\frac{15}{x}-\frac{9}{x^4}) $$

As $x$ approaches infinity, $\frac{15}{x}$ and $\frac{9}{x^4}$ approach 0.

$$ \lim_{x \to +\infty} x^4(3-\frac{15}{x}-\frac{9}{x^4}) = \lim_{x \to +\infty} x^4(3-0-0) = \lim_{x \to +\infty} 3x^4 = \infty $$

  1. Evaluate $\lim_{x \to +\infty} (3x^3-12x^2-10x-15)$

Factor out the highest power of $x$, which is $x^3$.

$$ \lim_{x \to +\infty} (3x^3-12x^2-10x-15) = \lim_{x \to +\infty} x^3(3-\frac{12}{x}-\frac{10}{x^2}-\frac{15}{x^3}) $$

As $x$ approaches infinity, $\frac{12}{x}$, $\frac{10}{x^2}$, and $\frac{15}{x^3}$ approach 0.

$$ \lim_{x \to +\infty} x^3(3-\frac{12}{x}-\frac{10}{x^2}-\frac{15}{x^3}) = \lim_{x \to +\infty} x^3(3-0-0-0) = \lim_{x \to +\infty} 3x^3 = \infty $$

  1. $\frac{5}{2}$
  2. $0$
  3. $\frac{4\sqrt{3}}{3}$
  4. $-1$
  5. $-\infty$
  6. $-\infty$
  7. $\infty$
  8. $\infty$

More Information

These problems involve evaluating limits at infinity. For rational functions, dividing by the highest power of $x$ in the denominator is a standard technique. For polynomials, factoring out the highest power of $x$ is useful. When $x$ approaches $-\infty$ and there is a square root, be careful with the sign when taking $x$ inside the square root.

Tips

A common mistake is to incorrectly handle the sign when $x$ approaches $-\infty$ inside a square root. For example, when dividing $\sqrt{x^2}$ by $x$ as $x \to -\infty$, $\frac{\sqrt{x^2}}{x} = -1$ and not $1$. Also, incorrectly identifying the dominant term will also cause the result to be incorrect.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!
Use Quizgecko on...
Browser
Open
Browser
Browser