Solve the following inequality: $\frac{2x}{x+3} + \frac{9}{x-2} \geq \frac{45}{x^2 + x - 6}$
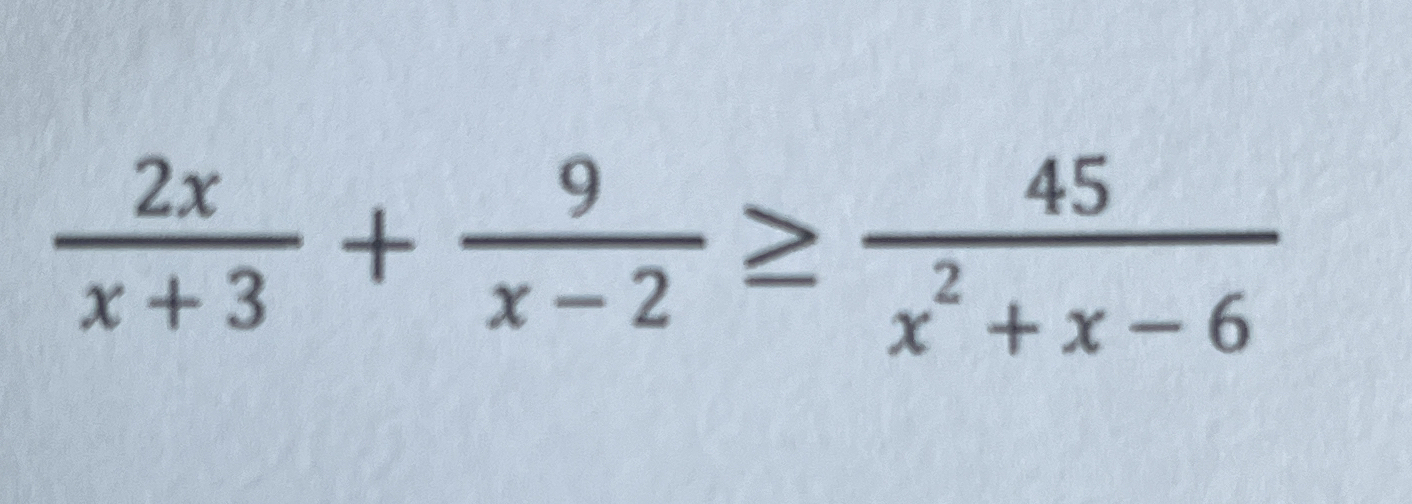
Understand the Problem
The question asks us to solve the inequality for $x$. This involves finding the common denominator, simplifying the inequality, and then determining the range of $x$ values that satisfy the inequality.
Answer
$x \in (-\infty, -\frac{9}{2}] \cup (-3, 2) \cup (2, \infty)$
Answer for screen readers
$x \in (-\infty, -\frac{9}{2}] \cup (-3, 2) \cup (2, \infty)$
Steps to Solve
-
Factor the quadratic expression
We need to factor the quadratic expression $x^2 + x - 6$. We look for two numbers that multiply to -6 and add to 1. These numbers are 3 and -2. Therefore, $x^2 + x - 6 = (x+3)(x-2)$.
-
Rewrite the inequality with the factored expression
The inequality can now be written as: $$ \frac{2x}{x+3} + \frac{9}{x-2} \geq \frac{45}{(x+3)(x-2)} $$
-
Identify restricted values
The denominators cannot be zero. Therefore, $x \neq -3$ and $x \neq 2$.
-
Combine the fractions on the left side
To combine the fractions on the left side, a common denominator is needed, which is $(x+3)(x-2)$. $$ \frac{2x(x-2)}{(x+3)(x-2)} + \frac{9(x+3)}{(x+3)(x-2)} \geq \frac{45}{(x+3)(x-2)} $$ $$ \frac{2x^2 - 4x + 9x + 27}{(x+3)(x-2)} \geq \frac{45}{(x+3)(x-2)} $$ $$ \frac{2x^2 + 5x + 27}{(x+3)(x-2)} \geq \frac{45}{(x+3)(x-2)} $$
-
Move all terms to one side
Subtract $\frac{45}{(x+3)(x-2)}$ from both sides: $$ \frac{2x^2 + 5x + 27}{(x+3)(x-2)} - \frac{45}{(x+3)(x-2)} \geq 0 $$ $$ \frac{2x^2 + 5x + 27 - 45}{(x+3)(x-2)} \geq 0 $$ $$ \frac{2x^2 + 5x - 18}{(x+3)(x-2)} \geq 0 $$
-
Factor the quadratic expression in the numerator
Factor the quadratic expression $2x^2 + 5x - 18$. We look for two numbers that multiply to $2 \cdot -18 = -36$ and add to 5. These numbers are 9 and -4. $$ 2x^2 - 4x + 9x - 18 = 2x(x-2) + 9(x-2) = (2x+9)(x-2) $$ The inequality becomes: $$ \frac{(2x+9)(x-2)}{(x+3)(x-2)} \geq 0 $$
-
Simplify the inequality
Since $x-2$ is a factor in both the numerator and the denominator, we can cancel it, but we must remember that $x \neq 2$: $$ \frac{2x+9}{x+3} \geq 0, \quad x \neq 2 $$
-
Find the critical points
The critical points are the values of $x$ that make the numerator or the denominator equal to zero. $2x+9 = 0 \Rightarrow x = -\frac{9}{2}$ $x+3 = 0 \Rightarrow x = -3$
-
Test the intervals
We have three critical points $-\frac{9}{2} = -4.5$, $-3$, and $2$. We need to test the intervals $(-\infty, -4.5]$, $(-4.5, -3)$, $(-3, 2)$, and $(2, \infty)$.
-
Interval $(-\infty, -4.5]$: Let $x = -5$. Then $\frac{2(-5)+9}{-5+3} = \frac{-10+9}{-2} = \frac{-1}{-2} = \frac{1}{2} > 0$. This interval satisfies the inequality.
-
Interval $(-4.5, -3)$: Let $x = -4$. Then $\frac{2(-4)+9}{-4+3} = \frac{-8+9}{-1} = \frac{1}{-1} = -1 < 0$. This interval does not satisfy the inequality.
-
Interval $(-3, 2)$: Let $x = 0$. Then $\frac{2(0)+9}{0+3} = \frac{9}{3} = 3 > 0$. This interval satisfies the inequality.
-
Interval $(2, \infty)$: Let $x = 3$. Then $\frac{2(3)+9}{3+3} = \frac{6+9}{6} = \frac{15}{6} = \frac{5}{2} > 0$. This interval satisfies the inequality.
-
-
Write the solution
The solution is $x \in (-\infty, -\frac{9}{2}] \cup (-3, 2) \cup (2, \infty)$.
$x \in (-\infty, -\frac{9}{2}] \cup (-3, 2) \cup (2, \infty)$
More Information
The solution to the inequality includes all values of $x$ less than or equal to $-\frac{9}{2}$, all values between $-3$ and $2$ (excluding $-3$ and including $2$), and all values greater than $2$ (excluding $2$). We exclude $x = -3$ and $x=2$ because they make the denominator zero, which is undefined.
Tips
- Forgetting to consider the restricted values: It is crucial to identify and exclude values of $x$ that make the denominator zero, such as $x=-3$ and $x=2$, as these values make the expression undefined.
- Incorrectly factoring or simplifying the inequality: Errors in factoring the quadratic expressions or simplifying the inequality can lead to an incorrect solution set.
- Not testing intervals properly: When testing intervals, picking numbers inside the interval is important to figure out where the inequality holds.
AI-generated content may contain errors. Please verify critical information