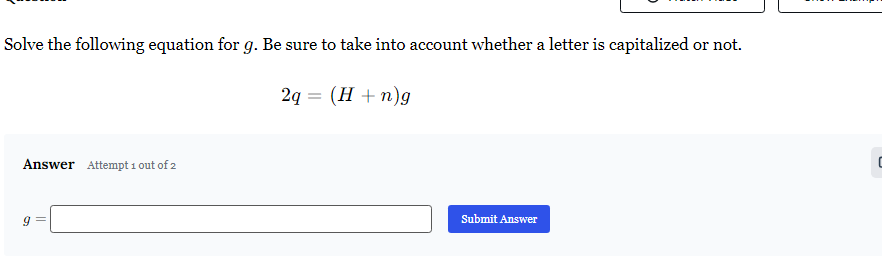
Solve the following equation for g: 2q = (H + n)g.

Understand the Problem

The question is asking us to solve the equation for the variable g, while considering the capitalization of the letters involved. This involves rearranging and isolating g on one side of the equation.

Answer

$$ g = \frac{2q}{H + n} $$

Steps to Solve

Identify the variables and constants

In the equation $2q = (H + n)g$, we have:

$2q$ on the left side
$(H + n)$ as a coefficient of $g$ on the right side.

Rearrange the equation to isolate g

To isolate $g$, we divide both sides by $(H + n)$: $$ g = \frac{2q}{H + n} $$

Final equation for g

This gives us the final equation for $g$: $$ g = \frac{2q}{H + n} $$

$$ g = \frac{2q}{H + n} $$

More Information

This equation expresses $g$ as a function of $q$, $H$, and $n$. It shows how the variable $g$ is affected by the values of these other variables.

Tips

Misinterpreting the equation: Ensure that (H + n) is treated as a single term in the denominator.
Forgetting to divide by the entire coefficient when isolating the variable: Always divide both sides by the whole term on the right side.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!