Solve the following equation for d: 4/3 d = g. Be sure to take into account whether a letter is capitalized or not.
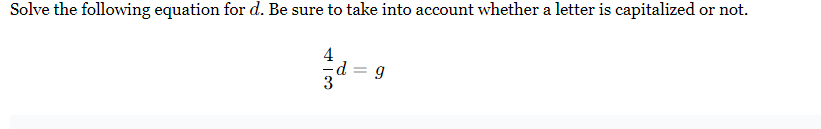
Understand the Problem
The question is asking to solve the equation \( \frac{4}{3}d = g \text{ for } d \text{ while considering capitalization of the letters. This involves isolating } d \text{ in the equation.}
Answer
The solution for \( d \) is $$ d = \frac{3}{4} g $$
Answer for screen readers
The final answer is
$$ d = \frac{3}{4} g $$
Steps to Solve
- Identify the equation The given equation is
$$ \frac{4}{3} d = g $$
- Isolate d To solve for ( d ), multiply both sides by the reciprocal of ( \frac{4}{3} ), which is ( \frac{3}{4} ):
$$ d = g \cdot \frac{3}{4} $$
- Final expression This simplifies to:
$$ d = \frac{3}{4} g $$
The final answer is
$$ d = \frac{3}{4} g $$
More Information
This equation shows that ( d ) is directly proportional to ( g ). This means that for every unit increase in ( g ), ( d ) increases by ( \frac{3}{4} ) of that unit. The capitalization of the letters indicates specific variables, which is important in algebra to differentiate between them.
Tips
- Incorrectly isolating the variable: A common mistake is failing to multiply by the correct reciprocal when isolating ( d ). Remember that multiplying by ( \frac{3}{4} ) is necessary to eliminate the fraction.
- Not considering capitalization: Ensure that you carefully differentiate between variables. ( d ) and ( g ) are distinct variables.
AI-generated content may contain errors. Please verify critical information