Solve the following differential equations using the method of variation of parameters: 1. y'' - 2y' + y = e^(2x) 2. y'' - 2y' - 3y = x + 2 3. y'' - 2y' + y = e^x / (1 + x^2) 4.... Solve the following differential equations using the method of variation of parameters: 1. y'' - 2y' + y = e^(2x) 2. y'' - 2y' - 3y = x + 2 3. y'' - 2y' + y = e^x / (1 + x^2) 4. y'' + 4y' + 4y = e^(-2x) / x^3
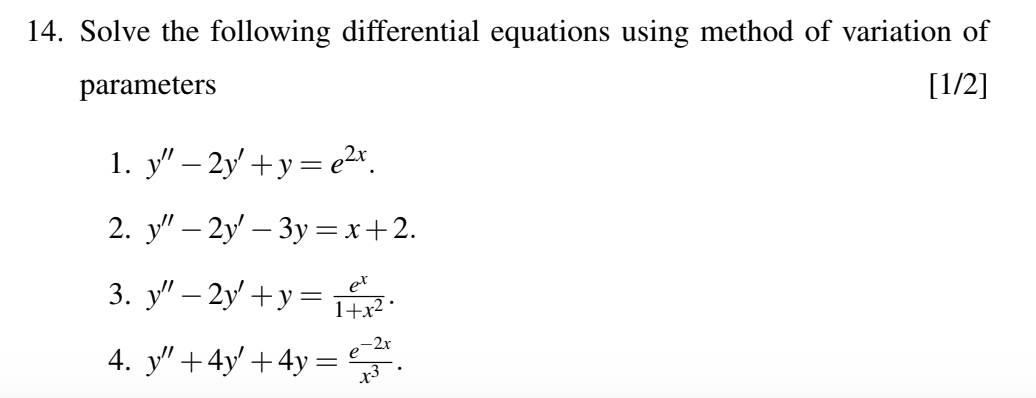
Understand the Problem
The question asks to solve four second-order non-homogeneous linear differential equations using the method of variation of parameters. This involves finding the homogeneous solution, then finding a particular solution using the variation of parameters technique, and finally combining them for the general solution.
Answer
1. $y = c_1 e^x + c_2 xe^x + e^{2x}$ 2. $y = c_1 e^{3x} + c_2 e^{-x} - \frac{1}{3}x - \frac{11}{18}$ 3. $y = c_1 e^x + c_2 xe^x - \frac{1}{2} e^x \ln(1+x^2) + xe^x \arctan(x)$ 4. $y = c_1 e^{-2x} + c_2 xe^{-2x} + \frac{1}{2x} e^{-2x}$
Answer for screen readers
- $ y = c_1 e^x + c_2 xe^x + e^{2x} $
- $ y = c_1 e^{3x} + c_2 e^{-x} - \frac{1}{3}x - \frac{11}{18} $
- $ y = c_1 e^x + c_2 xe^x - \frac{1}{2} e^x \ln(1+x^2) + xe^x \arctan(x) $
- $ y = c_1 e^{-2x} + c_2 xe^{-2x} + \frac{1}{2x} e^{-2x} $
Steps to Solve
- Solve the homogeneous equation for problem 1
The homogeneous equation is $ y'' - 2y' + y = 0 $. The characteristic equation is $ r^2 - 2r + 1 = 0 $, which factors to $ (r-1)^2 = 0 $. Thus, $ r = 1 $ is a repeated root. The homogeneous solution is $ y_h = c_1e^x + c_2xe^x $.
- Find the Wronskian for problem 1
Let $y_1 = e^x$ and $y_2 = xe^x$. The Wronskian is: $$ W = \begin{vmatrix} e^x & xe^x \ e^x & e^x + xe^x \end{vmatrix} = e^x(e^x + xe^x) - xe^x e^x = e^{2x} + xe^{2x} - xe^{2x} = e^{2x} $$
- Calculate $u_1'$ and $u_2'$ for problem 1 Using variation of parameters, $ y_p = u_1 y_1 + u_2 y_2 $ and we have:
$$ u_1' = -\frac{y_2 f(x)}{W} = -\frac{xe^x e^{2x}}{e^{2x}} = -xe^x $$ $$ u_2' = \frac{y_1 f(x)}{W} = \frac{e^x e^{2x}}{e^{2x}} = e^x $$
- Integrate to find $u_1$ and $u_2$ for problem 1
$$ u_1 = \int -xe^x dx = - \int xe^x dx $$ Using integration by parts, $ \int xe^x dx = xe^x - e^x $, so $ u_1 = -xe^x + e^x $.
$$ u_2 = \int e^x dx = e^x $$
- Form the particular solution for problem 1
$$ y_p = u_1 y_1 + u_2 y_2 = (-xe^x + e^x)e^x + (e^x)(xe^x) = -xe^{2x} + e^{2x} + xe^{2x} = e^{2x} $$
- Write the general solution for problem 1
$$ y = y_h + y_p = c_1 e^x + c_2 xe^x + e^{2x} $$
- Solve the homogeneous equation for problem 2
The homogeneous equation is $ y'' - 2y' - 3y = 0 $. The characteristic equation is $ r^2 - 2r - 3 = 0 $, which factors to $ (r-3)(r+1) = 0 $. Thus, $ r = 3, -1 $. The homogeneous solution is $ y_h = c_1e^{3x} + c_2e^{-x} $.
- Find the Wronskian for problem 2
Let $ y_1 = e^{3x} $ and $ y_2 = e^{-x} $. The Wronskian is: $$ W = \begin{vmatrix} e^{3x} & e^{-x} \ 3e^{3x} & -e^{-x} \end{vmatrix} = e^{3x}(-e^{-x}) - e^{-x}(3e^{3x}) = -e^{2x} - 3e^{2x} = -4e^{2x} $$
- Calculate $u_1'$ and $u_2'$ for problem 2 Using variation of parameters, $ y_p = u_1 y_1 + u_2 y_2 $ and we have $f(x) = x+2$:
$$ u_1' = -\frac{y_2 f(x)}{W} = -\frac{e^{-x}(x+2)}{-4e^{2x}} = \frac{x+2}{4e^{3x}} = \frac{1}{4} (x+2)e^{-3x} $$ $$ u_2' = \frac{y_1 f(x)}{W} = \frac{e^{3x}(x+2)}{-4e^{2x}} = -\frac{1}{4} (x+2)e^x $$
- Integrate to find $u_1$ and $u_2$ for problem 2
$$ u_1 = \int \frac{1}{4} (x+2)e^{-3x} dx = \frac{1}{4} \int (x+2)e^{-3x} dx $$ Using integration by parts, $ \int (x+2)e^{-3x} dx = -\frac{1}{3}(x+2)e^{-3x} - \frac{1}{9}e^{-3x} $. Thus, $ u_1 = \frac{1}{4} [-\frac{1}{3}(x+2)e^{-3x} - \frac{1}{9}e^{-3x}] = -\frac{1}{12}(x+2)e^{-3x} - \frac{1}{36}e^{-3x} $.
$$ u_2 = \int -\frac{1}{4} (x+2)e^x dx = -\frac{1}{4} \int (x+2)e^x dx $$ Using integration by parts, $ \int (x+2)e^x dx = (x+2)e^x - e^x $. Thus, $ u_2 = -\frac{1}{4} [(x+2)e^{x} - e^x] = -\frac{1}{4}(x+1)e^x $
- Form the particular solution for problem 2
$$ y_p = u_1 y_1 + u_2 y_2 = [-\frac{1}{12}(x+2)e^{-3x} - \frac{1}{36}e^{-3x}]e^{3x} + [-\frac{1}{4}(x+1)e^x]e^{-x} = -\frac{1}{12}x - \frac{2}{12} - \frac{1}{36} - \frac{1}{4}x - \frac{1}{4} = -\frac{1}{3}x - \frac{22}{36} = -\frac{1}{3}x - \frac{11}{18} $$
- Write the general solution for problem 2
$$ y = y_h + y_p = c_1 e^{3x} + c_2 e^{-x} - \frac{1}{3}x - \frac{11}{18} $$
- Solve the homogeneous equation for problem 3
The homogeneous equation is $ y'' - 2y' + y = 0 $. The characteristic equation is $ r^2 - 2r + 1 = 0 $, which factors to $ (r-1)^2 = 0 $. Thus, $ r = 1 $ is a repeated root. The homogeneous solution is $ y_h = c_1e^x + c_2xe^x $.
- Find the Wronskian for problem 3
Let $y_1 = e^x$ and $y_2 = xe^x$. The Wronskian is: $$ W = \begin{vmatrix} e^x & xe^x \ e^x & e^x + xe^x \end{vmatrix} = e^x(e^x + xe^x) - xe^x e^x = e^{2x} + xe^{2x} - xe^{2x} = e^{2x} $$
- Calculate $u_1'$ and $u_2'$ for problem 3 Using variation of parameters, $ y_p = u_1 y_1 + u_2 y_2 $ and we have $f(x) = \frac{e^x}{1+x^2}$:
$$ u_1' = -\frac{y_2 f(x)}{W} = -\frac{xe^x \frac{e^x}{1+x^2}}{e^{2x}} = -\frac{x}{1+x^2} $$ $$ u_2' = \frac{y_1 f(x)}{W} = \frac{e^x \frac{e^x}{1+x^2}}{e^{2x}} = \frac{1}{1+x^2} $$
- Integrate to find $u_1$ and $u_2$ for problem 3
$$ u_1 = \int -\frac{x}{1+x^2} dx = -\frac{1}{2} \ln(1+x^2) $$ $$ u_2 = \int \frac{1}{1+x^2} dx = \arctan(x) $$
- Form the particular solution for problem 3
$$ y_p = u_1 y_1 + u_2 y_2 = (-\frac{1}{2} \ln(1+x^2))e^x + (\arctan(x)) xe^x $$
- Write the general solution for problem 3
$$ y = y_h + y_p = c_1 e^x + c_2 xe^x - \frac{1}{2} e^x \ln(1+x^2) + xe^x \arctan(x) $$
- Solve the homogeneous equation for problem 4
The homogeneous equation is $ y'' + 4y' + 4y = 0 $. The characteristic equation is $ r^2 + 4r + 4 = 0 $, which factors to $ (r+2)^2 = 0 $. Thus, $ r = -2 $ is a repeated root. The homogeneous solution is $ y_h = c_1 e^{-2x} + c_2 xe^{-2x} $.
- Find the Wronskian for problem 4
Let $y_1 = e^{-2x}$ and $y_2 = xe^{-2x}$. The Wronskian is: $$ W = \begin{vmatrix} e^{-2x} & xe^{-2x} \ -2e^{-2x} & e^{-2x} - 2xe^{-2x} \end{vmatrix} = e^{-2x}(e^{-2x} - 2xe^{-2x}) - xe^{-2x}(-2e^{-2x}) = e^{-4x} - 2xe^{-4x} + 2xe^{-4x} = e^{-4x} $$
- Calculate $u_1'$ and $u_2'$ for problem 4 Using variation of parameters, $ y_p = u_1 y_1 + u_2 y_2 $ and we have $f(x) = \frac{e^{-2x}}{x^3}$:
$$ u_1' = -\frac{y_2 f(x)}{W} = -\frac{xe^{-2x} \frac{e^{-2x}}{x^3}}{e^{-4x}} = -\frac{1}{x^2} $$ $$ u_2' = \frac{y_1 f(x)}{W} = \frac{e^{-2x} \frac{e^{-2x}}{x^3}}{e^{-4x}} = \frac{1}{x^3} $$
- Integrate to find $u_1$ and $u_2$ for problem 4
$$ u_1 = \int -\frac{1}{x^2} dx = \frac{1}{x} $$ $$ u_2 = \int \frac{1}{x^3} dx = -\frac{1}{2x^2} $$
- Form the particular solution for problem 4
$$ y_p = u_1 y_1 + u_2 y_2 = (\frac{1}{x})e^{-2x} + (-\frac{1}{2x^2}) xe^{-2x} = \frac{1}{x}e^{-2x} - \frac{1}{2x}e^{-2x} = \frac{1}{2x} e^{-2x} $$
- Write the general solution for problem 4
$$ y = y_h + y_p = c_1 e^{-2x} + c_2 xe^{-2x} + \frac{1}{2x} e^{-2x} $$
- $ y = c_1 e^x + c_2 xe^x + e^{2x} $
- $ y = c_1 e^{3x} + c_2 e^{-x} - \frac{1}{3}x - \frac{11}{18} $
- $ y = c_1 e^x + c_2 xe^x - \frac{1}{2} e^x \ln(1+x^2) + xe^x \arctan(x) $
- $ y = c_1 e^{-2x} + c_2 xe^{-2x} + \frac{1}{2x} e^{-2x} $
More Information
Variation of parameters is a powerful technique for solving non-homogeneous linear differential equations, especially when the forcing function (the right-hand side of the equation) doesn't allow for simple solutions via undetermined coefficients.
Tips
- Forgetting to include both linearly independent solutions in the homogeneous solution when dealing with repeated roots.
- Incorrectly calculating the Wronskian.
- Making errors during integration by parts.
AI-generated content may contain errors. Please verify critical information