Solve the equation (x + y) / (x - y) - (x - y) / (x + y) = 2xy / (x^2 - y^2)
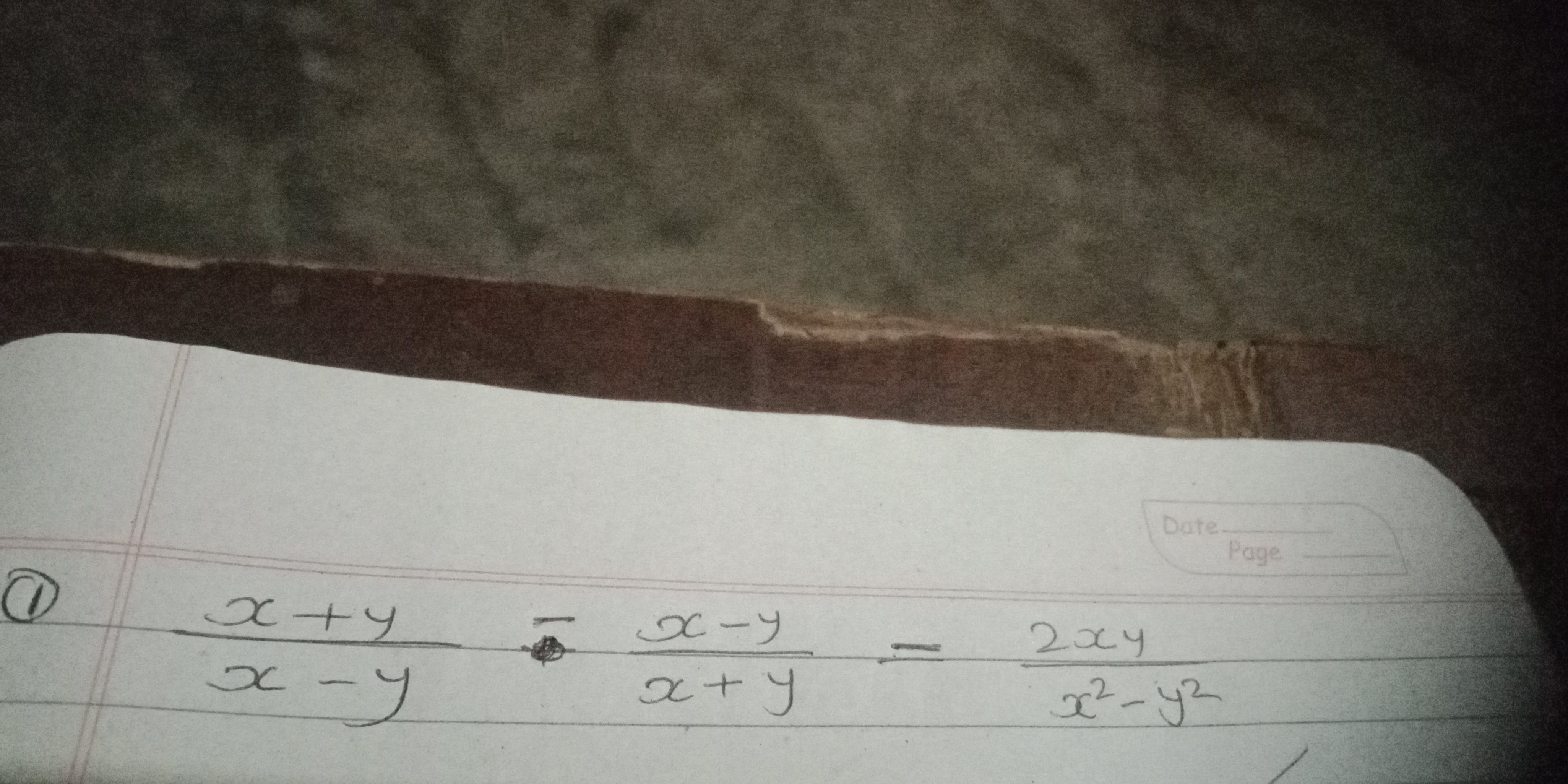
Understand the Problem
The question is a mathematical expression involving fractions and variables x and y. It appears to be asking for simplification or solving of the given equation.
Answer
No solution.
Answer for screen readers
There is no solution to the equation since it leads to a contradiction.
Steps to Solve
-
Combine the fractions on the left side To combine the fractions ( \frac{x + y}{x - y} - \frac{x - y}{x + y} ), find a common denominator, which is ( (x - y)(x + y) ): [ \frac{(x + y)^2 - (x - y)^2}{(x - y)(x + y)} ]
-
Expand the numerators Now expand the numerators:
- ( (x + y)^2 = x^2 + 2xy + y^2 )
- ( (x - y)^2 = x^2 - 2xy + y^2 )
Substituting back in gives: [ \frac{(x^2 + 2xy + y^2) - (x^2 - 2xy + y^2)}{(x - y)(x + y)} ]
-
Simplify the numerator Simplifying the numerator: [ x^2 + 2xy + y^2 - x^2 + 2xy - y^2 = 4xy ] Thus, we have: [ \frac{4xy}{(x - y)(x + y)} ]
-
Set the equation with the right side Now our equation reads: [ \frac{4xy}{(x - y)(x + y)} = \frac{2xy}{x^2 - y^2} ]
-
Recognize that ( x^2 - y^2 = (x - y)(x + y) ) Replace ( x^2 - y^2 ) in the right side: [ \frac{4xy}{(x - y)(x + y)} = \frac{2xy}{(x - y)(x + y)} ]
-
Cross multiply Cross-multiply to eliminate the fractions: [ 4xy \cdot (x - y)(x + y) = 2xy \cdot (x - y)(x + y) ]
-
Simplify the equation Since ( (x - y)(x + y) ) is common on both sides and can be divided out (assuming ( x \neq y )): [ 4xy = 2xy ]
-
Divide both sides by ( 2xy ) (assuming ( xy \neq 0 )) This simplifies to: [ 2 = 1 ] This means there's no solution under the assumption that both sides are equal.
There is no solution to the equation since it leads to a contradiction.
More Information
When both sides of an equation simplify to an impossible statement like ( 2 = 1 ), that indicates the original equation does not have any values of ( x ) and ( y ) that satisfy it under normal circumstances.
Tips
- Assuming ( x = y ) without recognizing that it leads to division by zero.
- Forgetting to simplify the numerators correctly when combining fractions.
AI-generated content may contain errors. Please verify critical information