Solve the equation e^t - t sin(2t).
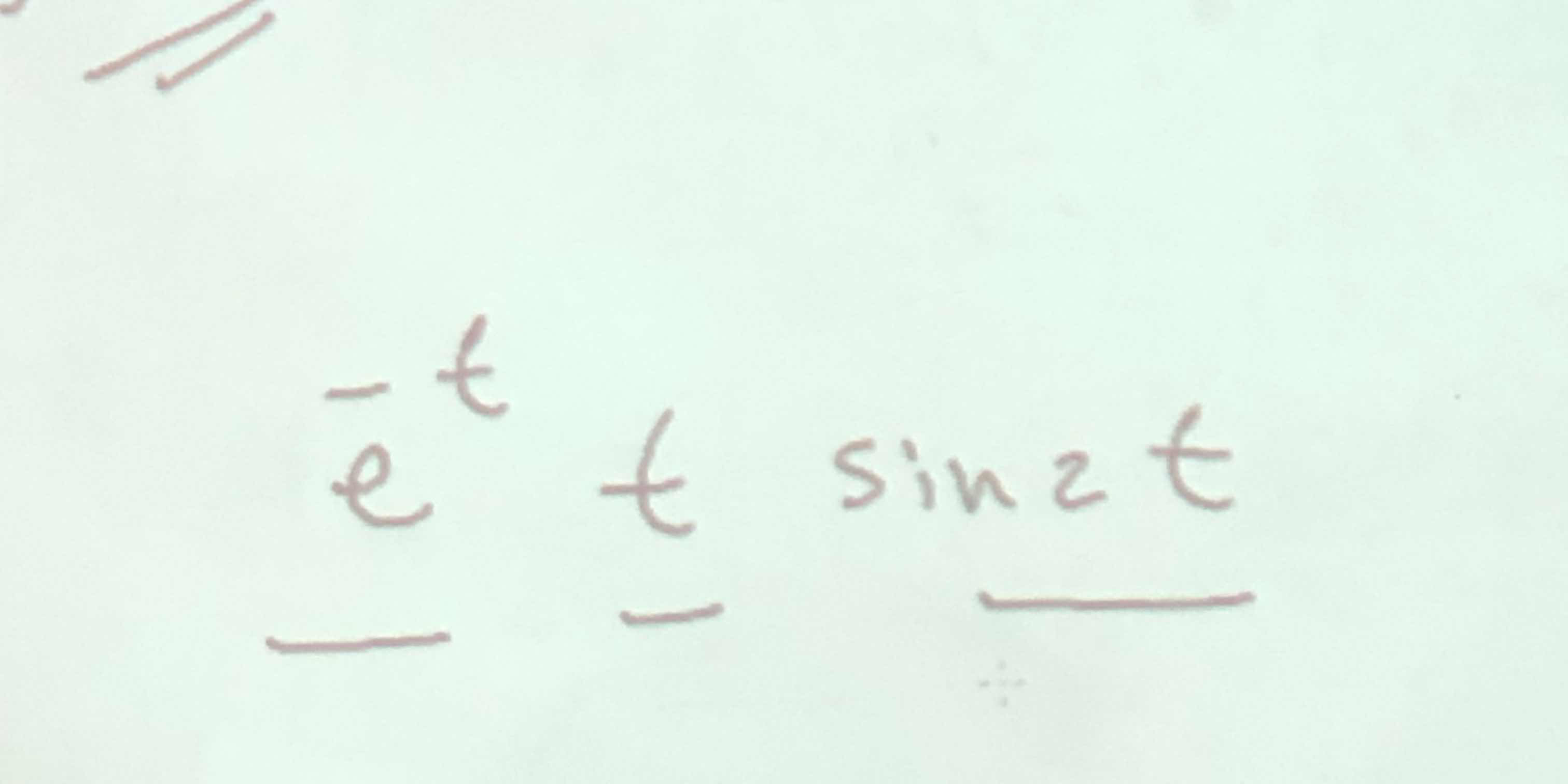
Understand the Problem
The question appears to be related to a mathematical expression involving 'e' (the base of natural logarithms) and 'sin' (the sine function). It seems to require solving or simplifying the equation represented in the image.
Answer
The derivative is \( e^t - \sin(2t) - 2t \cos(2t) \).
Answer for screen readers
The derivative of the expression ( e^t - t \sin(2t) ) is: $$ e^t - \sin(2t) - 2t \cos(2t) $$
Steps to Solve
-
Identify the expression
The expression given is ( e^t - t \sin(2t) ). -
Analyze derivative if needed
If we are interested in the behavior of this expression, we can find the derivative. The derivative ( \frac{d}{dt} ) can be computed separately for both terms.The derivative of ( e^t ) is ( e^t ).
The derivative of ( -t \sin(2t) ) requires the product rule:
If ( u = t ) and ( v = \sin(2t) ), then: $$ \frac{d}{dt}(-t \sin(2t)) = -\left( \sin(2t) + t \cdot 2 \cos(2t) \right) $$ Thus, $$ = -\sin(2t) - 2t \cos(2t) $$ -
Combine results
So the full derivative of the expression is: $$ \frac{d}{dt}(e^t - t \sin(2t)) = e^t - \sin(2t) - 2t \cos(2t) $$ -
Conclusion
The expression ( e^t - t \sin(2t) ) behaves according to the above derivative.
The derivative of the expression ( e^t - t \sin(2t) ) is: $$ e^t - \sin(2t) - 2t \cos(2t) $$
More Information
This expression involves both exponential growth through ( e^t ) and oscillatory behavior through the sine function. The derivative we found helps in understanding how the expression behaves over time.
Tips
- Forgetting the product rule: Many might overlook the application of the product rule when differentiating terms like ( -t \sin(2t) ).
- Incorrectly computing the derivatives: Ensure to take care of the coefficients and additional multiplicative factors during differentiation.
AI-generated content may contain errors. Please verify critical information