Solve the equation √(4 + √x) = 5 for X.
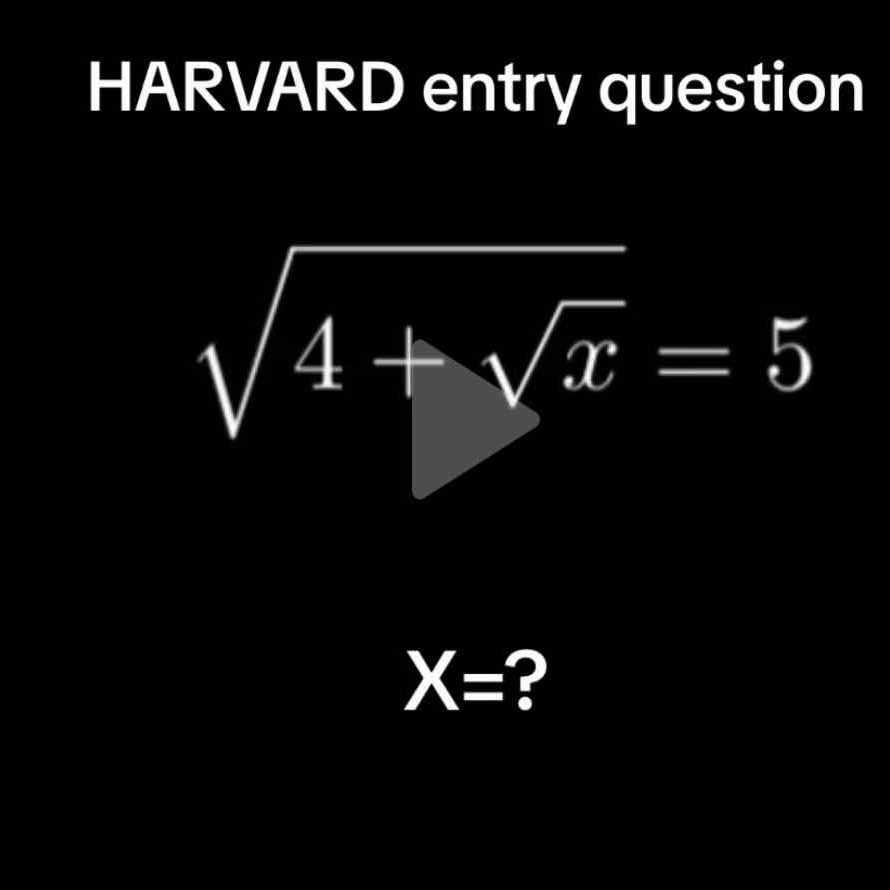
Understand the Problem
The question is asking to solve the equation involving a square root for the variable X. The equation given is √(4 + √x) = 5, and we need to determine the value of X.
Answer
The value of $x$ is $441$.
Answer for screen readers
The value of $x$ is $441$.
Steps to Solve
- Isolate the square root expression
First, start with the original equation:
$$ \sqrt{4 + \sqrt{x}} = 5 $$
To eliminate the square root, square both sides:
$$ 4 + \sqrt{x} = 5^2 $$
- Calculate the square
Calculating the right side:
$$ 5^2 = 25 $$
Substituting this back into the equation gives:
$$ 4 + \sqrt{x} = 25 $$
- Solve for $\sqrt{x}$
Next, isolate $\sqrt{x}$ by subtracting 4 from both sides:
$$ \sqrt{x} = 25 - 4 $$
This simplifies to:
$$ \sqrt{x} = 21 $$
- Square both sides again to solve for x
Now, square both sides to solve for $x$:
$$ x = (21)^2 $$
Calculating the square:
$$ x = 441 $$
The value of $x$ is $441$.
More Information
The initial equation involves nested square roots, making it essential to isolate and square carefully to avoid errors. The final result shows that $441$ is the solution to the equation.
Tips
- Forgetting to square both sides of the equation correctly, which could lead to incorrect values.
- Not isolating the square root before squaring, which can complicate the solution.
- Miscalculating $21^2$ and obtaining the wrong answer.
AI-generated content may contain errors. Please verify critical information