Solve the equation $2 = x^2 + 10x + 21$
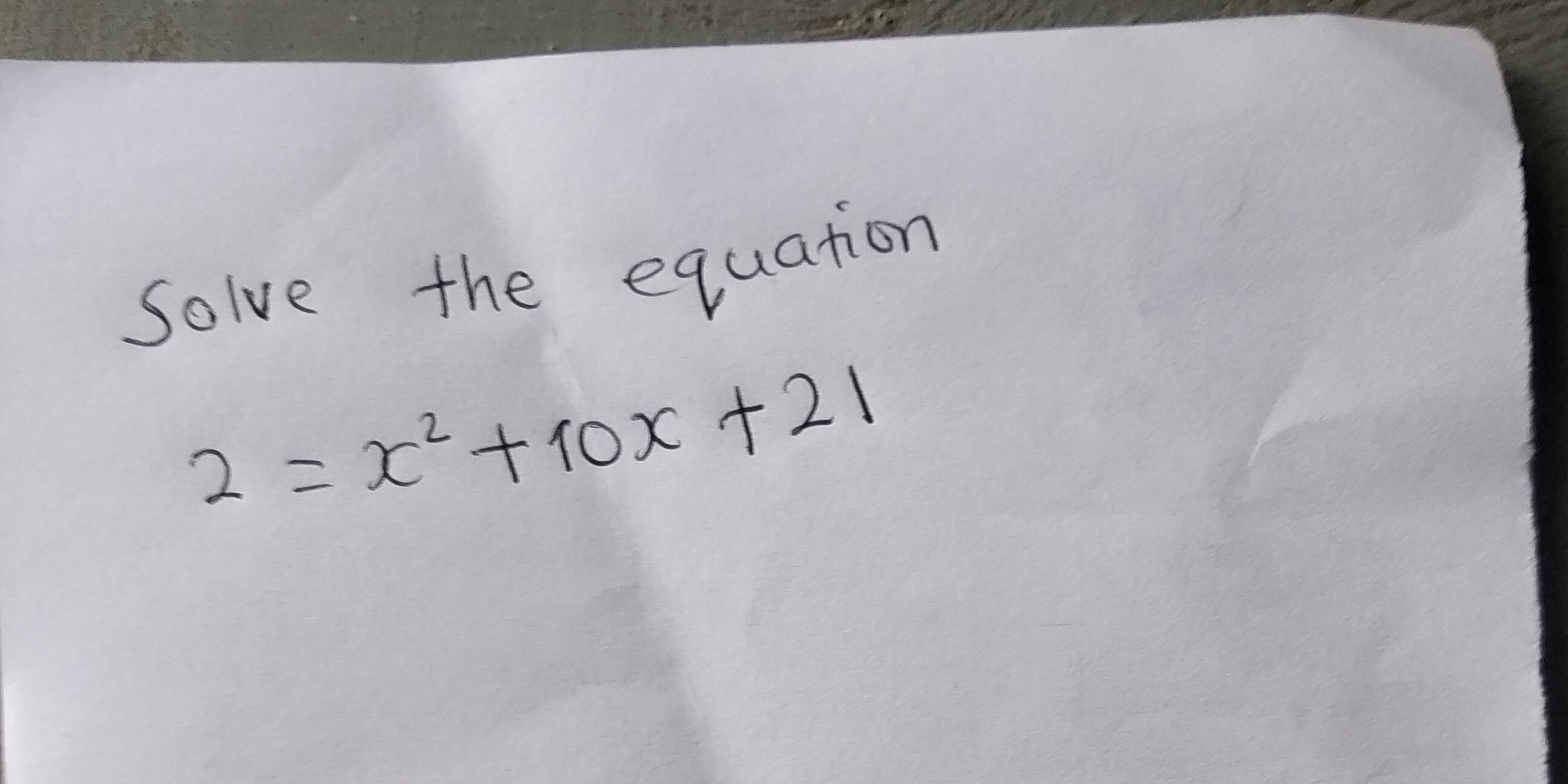
Understand the Problem
The question asks to solve the quadratic equation $2 = x^2 + 10x + 21$. This involves rearranging the equation to the standard quadratic form and then finding the roots, which can be done by factoring, completing the square, or using the quadratic formula.
Answer
$x = -5 \pm \sqrt{6}$
Answer for screen readers
$x = -5 + \sqrt{6}$ or $x = -5 - \sqrt{6}$
Steps to Solve
-
Rearrange the equation Subtract 2 from both sides of the equation to set it to zero: $2 - 2 = x^2 + 10x + 21 - 2$ $0 = x^2 + 10x + 19$
-
Solve using the quadratic formula The quadratic formula is $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, where $a = 1$, $b = 10$, and $c = 19$ in the quadratic equation $ax^2 + bx + c = 0$.
-
Plug the values into the quadratic formula $x = \frac{-10 \pm \sqrt{10^2 - 4(1)(19)}}{2(1)}$ $x = \frac{-10 \pm \sqrt{100 - 76}}{2}$ $x = \frac{-10 \pm \sqrt{24}}{2}$
-
Simplify the square root $\sqrt{24}$ can be simplified to $\sqrt{4 \cdot 6} = 2\sqrt{6}$
-
Substitute back into the equation $x = \frac{-10 \pm 2\sqrt{6}}{2}$
-
Simplify the expression Divide both terms in the numerator by 2: $x = -5 \pm \sqrt{6}$
$x = -5 + \sqrt{6}$ or $x = -5 - \sqrt{6}$
More Information
The roots of the quadratic equation $2 = x^2 + 10x + 21$ are $x = -5 + \sqrt{6}$ and $x = -5 - \sqrt{6}$. These are the $x$-intercepts of the parabola $y = x^2 + 10x + 19$.
Tips
A common mistake is to incorrectly apply the quadratic formula, such as misidentifying the coefficients $a$, $b$, and $c$, or making errors in the arithmetic. Another common mistake is not simplifying the square root correctly. To avoid these mistakes, carefully write down each value and double-check your calculations.
AI-generated content may contain errors. Please verify critical information