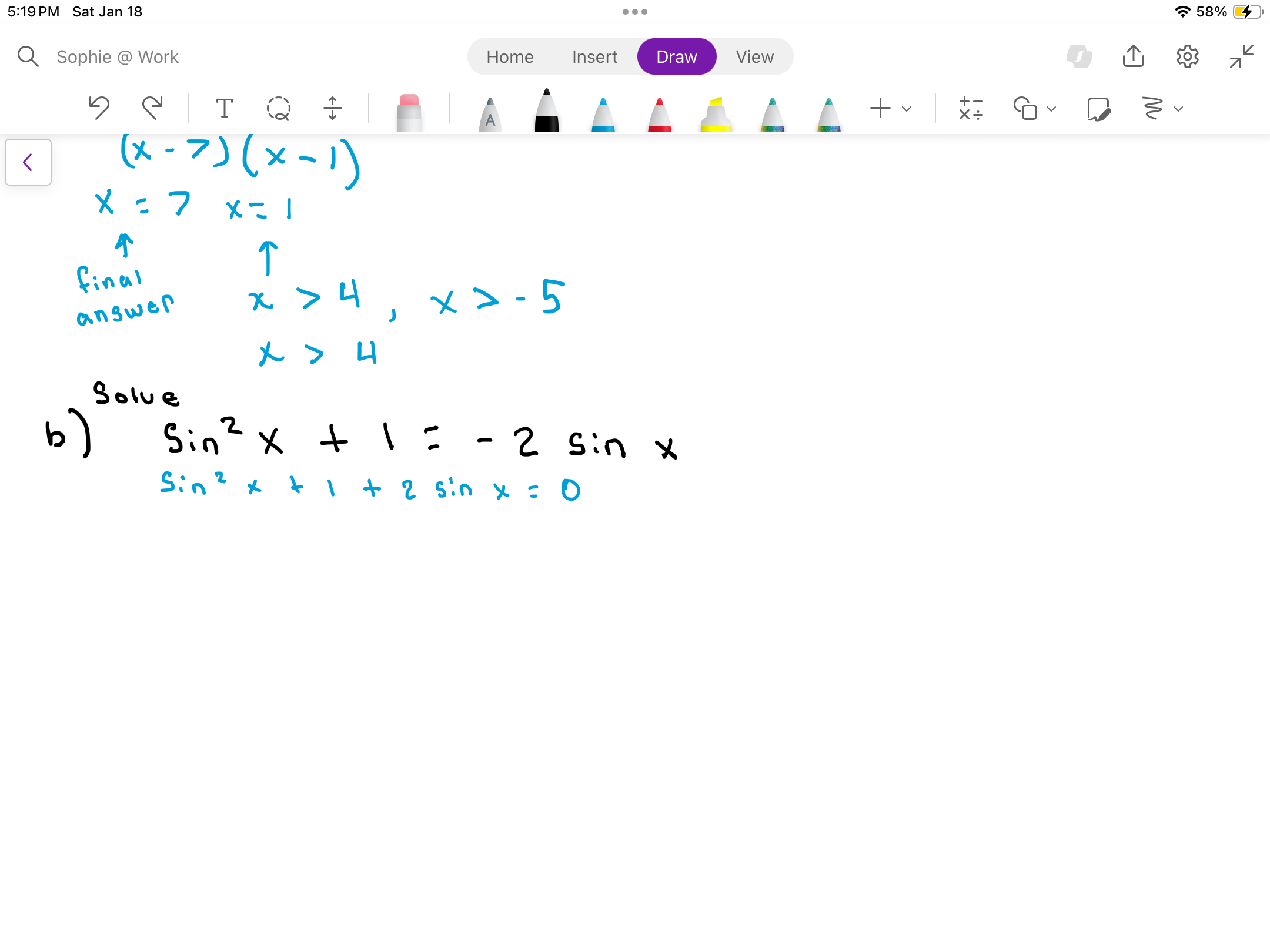
Solve Sin²(x) + 1 = -2 Sin(x).
Understand the Problem
The question is asking to solve the equation Sin²(x) + 1 = -2 Sin(x), which implies rewriting and simplifying the equation to find the values of x.
Answer
The solutions are: $$x = \frac{3\pi}{2} + 2k\pi, \quad k \in \mathbb{Z}$$
Answer for screen readers
The solutions are:
$$x = \frac{3\pi}{2} + 2k\pi, \quad k \in \mathbb{Z}$$
Steps to Solve
-
Rewrite the equation
Starting with the original equation:
$$\sin^2 x + 1 = -2 \sin x$$
We can rearrange this to:
$$\sin^2 x + 2 \sin x + 1 = 0$$ -
Recognize the quadratic form
The rearranged equation is a quadratic equation in the form:
$$a \sin^2 x + b \sin x + c = 0$$
Here, we have:
- $a = 1$
- $b = 2$
- $c = 1$
-
Factoring the quadratic
We can factor the quadratic equation:
$$(\sin x + 1)(\sin x + 1) = 0$$
or simply:
$$(\sin x + 1)^2 = 0$$ -
Setting the factored form to zero
To find the values of $\sin x$:
$$\sin x + 1 = 0$$
This implies:
$$\sin x = -1$$ -
Finding solutions
The solutions for $\sin x = -1$ occur at:
$$x = \frac{3\pi}{2} + 2k\pi$$
where $k$ is any integer.
The solutions are:
$$x = \frac{3\pi}{2} + 2k\pi, \quad k \in \mathbb{Z}$$
More Information
The solution $\sin x = -1$ corresponds to angles where the sine function achieves its minimum value on the unit circle. The general solution accounts for the periodic nature of trigonometric functions.
Tips
- Forgetting to consider the periodic nature of the sine function, which can lead to missing out on additional solutions.
- Incorrectly factoring the quadratic equation.
AI-generated content may contain errors. Please verify critical information