Solve for x: x^4 / (x + x + x) = 72, where x ≠ 0.
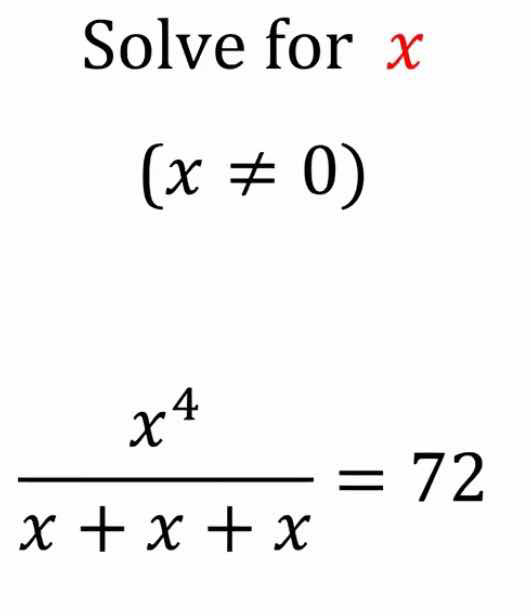
Understand the Problem
The question is asking us to solve the equation for x. The equation provided involves a fraction with x raised to the power of 4 in the numerator and a linear expression in the denominator. The goal is to isolate x and find its value.
Answer
The value of \( x \) is \( 6 \).
Answer for screen readers
The solution for ( x ) is ( x = 6 ).
Steps to Solve
-
Simplify the denominator The denominator ( x + x + x ) can be simplified. This simplifies to ( 3x ).
-
Rewrite the equation Substituting the simplified denominator into the equation: $$ \frac{x^{4}}{3x} = 72 $$
-
Multiply both sides by the denominator To eliminate the fraction, multiply both sides by ( 3x ) (noting ( x \neq 0 )): $$ x^{4} = 72 \cdot 3x $$
-
Calculate the right side Compute ( 72 \times 3 ): $$ 72 \cdot 3 = 216 $$ So the equation becomes: $$ x^{4} = 216x $$
-
Rearrange the equation Move ( 216x ) to the left side to set the equation to zero: $$ x^{4} - 216x = 0 $$
-
Factor the equation Factor out ( x ): $$ x(x^{3} - 216) = 0 $$
-
Set each factor to zero This gives us two cases to solve:
- ( x = 0 ) (not valid since ( x \neq 0 ))
- ( x^{3} - 216 = 0 )
- Solve for ( x ) Solving ( x^{3} - 216 = 0 ): $$ x^{3} = 216 $$ Taking the cube root of both sides: $$ x = \sqrt[3]{216} = 6 $$
The solution for ( x ) is ( x = 6 ).
More Information
The original equation simplifies to one where ( x^{3} = 216 ). The cube root of 216 is 6. This type of equation often appears in algebra when working with polynomials and simplifying rational expressions.
Tips
- Neglecting the simplification of the denominator: Always simplify the expression before solving.
- Not factoring correctly: Make sure to correctly factor out common terms, as done with ( x ).
AI-generated content may contain errors. Please verify critical information