Solve for x: $x^3 - x^2 - 2x = 0$
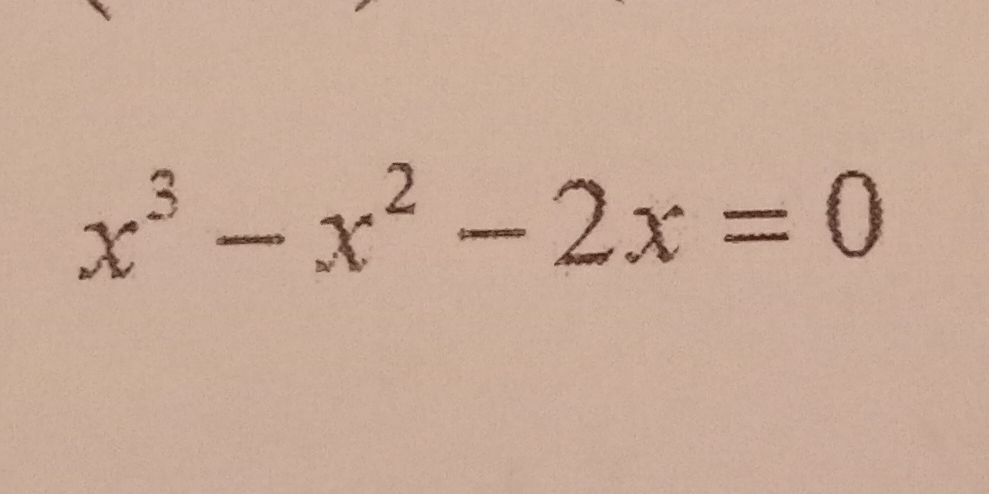
Understand the Problem
The question presents a cubic equation, $x^3 - x^2 - 2x = 0$, and asks to find the values of x that satisfy the equation. This requires factoring and solving for the roots.
Answer
$x = -1, 0, 2$
Answer for screen readers
$x = -1, 0, 2$
Steps to Solve
- Factor out the common term $x$
The first step is to factor out the common term $x$ from the equation $x^3 - x^2 - 2x = 0$. This gives us: $x(x^2 - x - 2) = 0$
- Factor the quadratic expression
Now, we need to factor the quadratic expression $x^2 - x - 2$. We are looking for two numbers that multiply to -2 and add to -1. These numbers are -2 and 1. So, we can factor the quadratic as:
$x^2 - x - 2 = (x - 2)(x + 1)$
- Rewrite the equation
Now substitute the factored quadratic back into the equation:
$x(x - 2)(x + 1) = 0$
- Solve for $x$
To find the values of $x$ that satisfy the equation, we set each factor equal to zero:
$x = 0$ $x - 2 = 0 \implies x = 2$ $x + 1 = 0 \implies x = -1$
Thus, the solutions are $x = 0$, $x = 2$, and $x = -1$.
$x = -1, 0, 2$
More Information
The given cubic equation has three real roots: -1, 0, and 2. This is because a cubic equation can have up to three real roots.
Tips
A common mistake is to divide the equation by $x$ in the beginning. This would lead to losing the root $x=0$. It is important to factor instead of dividing when solving for roots. Another mistake is incorrectly factoring the quadratic equation. Always double-check your factors by expanding them to ensure they match the original quadratic.
AI-generated content may contain errors. Please verify critical information