Solve for x: $(x^2 - 3x + 1)^{(2x^2 + x - 6)} = 1$
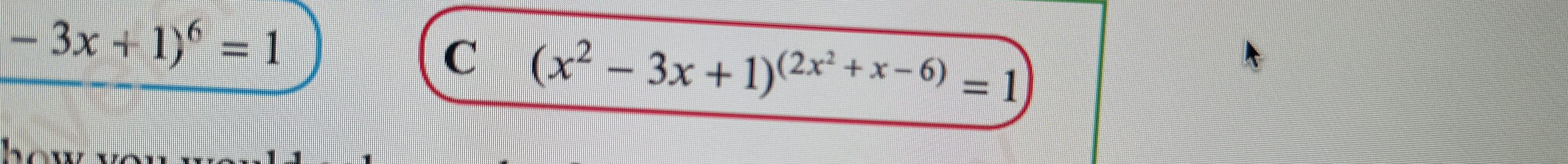
Understand the Problem
The question is asking to solve the equation $(x^2 - 3x + 1)^{(2x^2 + x - 6)} = 1$ for $x$. We need to find the values of $x$ that satisfy this equation.
Answer
$x = -2, 0, \frac{3}{2}, 2, 3$
Answer for screen readers
$x = -2, 0, \frac{3}{2}, 2, 3$
Steps to Solve
-
Case 1: The exponent is zero If the exponent $2x^2 + x - 6 = 0$ and the base $x^2 - 3x + 1 \neq 0$, then the equation becomes $1$.
-
Solve the quadratic exponent equation Solve $2x^2 + x - 6 = 0$: $$2x^2 + x - 6 = 0$$ $$(2x - 3)(x + 2) = 0$$ $$x = \frac{3}{2}, -2$$
-
Check the base for $x = \frac{3}{2}$ For $x = \frac{3}{2}$: $$(\frac{3}{2})^2 - 3(\frac{3}{2}) + 1 = \frac{9}{4} - \frac{9}{2} + 1 = \frac{9 - 18 + 4}{4} = \frac{-5}{4} \neq 0$$ Hence $x = \frac{3}{2}$ is a solution.
-
Check the base for $x = -2$ For $x = -2$: $$(-2)^2 - 3(-2) + 1 = 4 + 6 + 1 = 11 \neq 0$$ Hence $x = -2$ is a solution.
-
Case 2: The base is one If the base $x^2 - 3x + 1 = 1$, then the equation becomes $1$ regardless of the exponent.
-
Solve the quadratic base equation Solve $x^2 - 3x + 1 = 1$: $$x^2 - 3x = 0$$ $$x(x - 3) = 0$$ $$x = 0, 3$$
-
Case 3: The base is negative one and the exponent is even If the base $x^2 - 3x + 1 = -1$ and the exponent $2x^2 + x - 6$ is an even integer, then the equation becomes $1$.
-
Solve the quadratic base equation Solve $x^2 - 3x + 1 = -1$: $$x^2 - 3x + 2 = 0$$ $$(x - 1)(x - 2) = 0$$ $$x = 1, 2$$
-
Check the exponent for $x = 1$ For $x = 1$: $$2(1)^2 + 1 - 6 = 2 + 1 - 6 = -3$$ $-3$ is odd, so $x = 1$ is not a solution.
-
Check the exponent for $x = 2$ For $x = 2$: $$2(2)^2 + 2 - 6 = 8 + 2 - 6 = 4$$ $4$ is even, so $x = 2$ is a solution.
-
Gather all solutions The solutions are $x = -2, 0, \frac{3}{2}, 2, 3$.
$x = -2, 0, \frac{3}{2}, 2, 3$
More Information
The problem involves considering different cases where an exponential expression equals one. It is important to check all solutions by plugging them back into the original equation.
Tips
A common mistake is forgetting to consider the case where the base is -1 and the exponent is even. Also, students might forget to check if the base is zero when the exponent is zero, which would make the expression undefined. Not considering all cases or making algebraic errors while solving the quadratic equations are also common mistakes.
AI-generated content may contain errors. Please verify critical information