Solve for x: (x-1)/(x+2) = (2x-5)/(x-1)
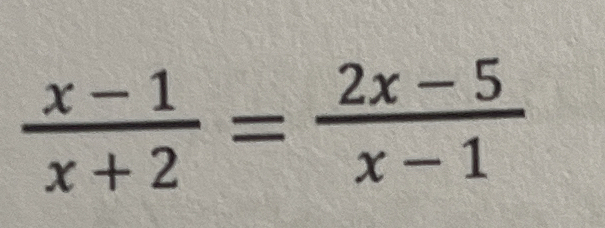
Understand the Problem
The question requires us to solve for x in the given equation involving rational expressions. We'll need to cross-multiply, simplify the resulting polynomial equation, and then find the value(s) of x that satisfy the equation.
Answer
$x = \frac{-1 \pm 3\sqrt{5}}{2}$
Answer for screen readers
$x = \frac{-1 + 3\sqrt{5}}{2}$ or $x = \frac{-1 - 3\sqrt{5}}{2}$
Steps to Solve
- Cross-multiply
Cross-multiply to get rid of the fractions.
$$(x-1)(x-1) = (2x-5)(x+2)$$
- Expand both sides
Expand both sides of the equation.
$$x^2 - 2x + 1 = 2x^2 + 4x - 5x - 10$$
$$x^2 - 2x + 1 = 2x^2 - x - 10$$
- Rearrange the equation
Move all terms to one side to set the equation to zero.
$$0 = 2x^2 - x - 10 - x^2 + 2x - 1$$
$$0 = x^2 + x - 11$$
- Solve the quadratic equation
Use the quadratic formula to solve for $x$: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
In our case, we have $a=1$, $b=1$, and $c=-11$.
$$x = \frac{-1 \pm \sqrt{1^2 - 4(1)(-11)}}{2(1)}$$
$$x = \frac{-1 \pm \sqrt{1 + 44}}{2}$$
$$x = \frac{-1 \pm \sqrt{45}}{2}$$
$$x = \frac{-1 \pm 3\sqrt{5}}{2}$$
$x = \frac{-1 + 3\sqrt{5}}{2}$ or $x = \frac{-1 - 3\sqrt{5}}{2}$
More Information
The solutions are irrational numbers. We can approximate these values as $x \approx 2.85$ or $x \approx -3.85$.
Tips
- Incorrectly expanding the expressions: Make sure to distribute correctly when expanding $(x-1)(x-1)$ and $(2x-5)(x+2)$.
- Sign errors: Be careful with signs when rearranging the equation and applying the quadratic formula.
- Forgetting to check for extraneous solutions: Although not explicitly required here, always check your solutions in the original equation to make sure they don't make any denominators zero (especially $x = -2$ or $x = 1$). In this case, neither solution makes the denominator zero, so both are valid.
AI-generated content may contain errors. Please verify critical information