Solve for x: log_4(x) = -1/2
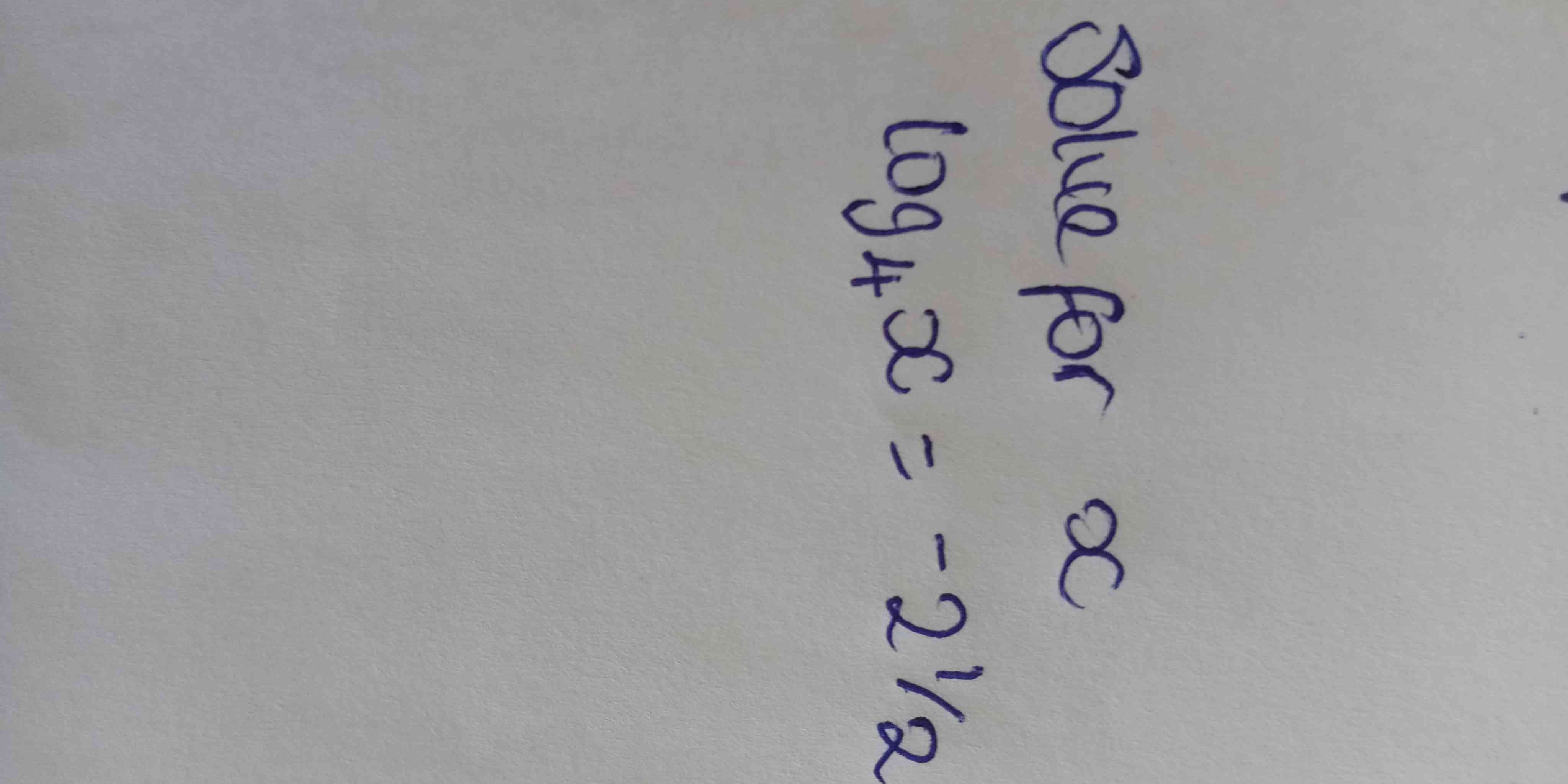
Understand the Problem
The question asks to solve for x in the logarithmic equation log base 4 of x = -1/2. To solve for x, we need to convert the logarithmic equation into an exponential equation.
Answer
$x = \frac{1}{2}$
Answer for screen readers
$x = \frac{1}{2}$
Steps to Solve
- Rewrite the logarithmic equation in exponential form
The logarithmic equation $\log_4{x} = -\frac{1}{2}$ can be rewritten in exponential form as $4^{-\frac{1}{2}} = x$.
- Simplify the exponential expression
Recall that $a^{-\frac{1}{2}} = \frac{1}{a^{\frac{1}{2}}} = \frac{1}{\sqrt{a}}$. Applying this to our equation, we have $x = 4^{-\frac{1}{2}} = \frac{1}{\sqrt{4}}$.
- Evaluate the square root
Since $\sqrt{4} = 2$, we have $x = \frac{1}{2}$.
$x = \frac{1}{2}$
More Information
The solution $x = \frac{1}{2}$ means that 4 raised to the power of $-\frac{1}{2}$ equals $\frac{1}{2}$.
Tips
A common mistake is to incorrectly apply the negative exponent or miscalculate the square root. Remember that a negative exponent indicates a reciprocal, and a fractional exponent indicates a root.
AI-generated content may contain errors. Please verify critical information