Solve for x: $\frac{4x}{x-1} - \frac{3}{x+2} = \frac{12}{(x+2)(x-1)}$
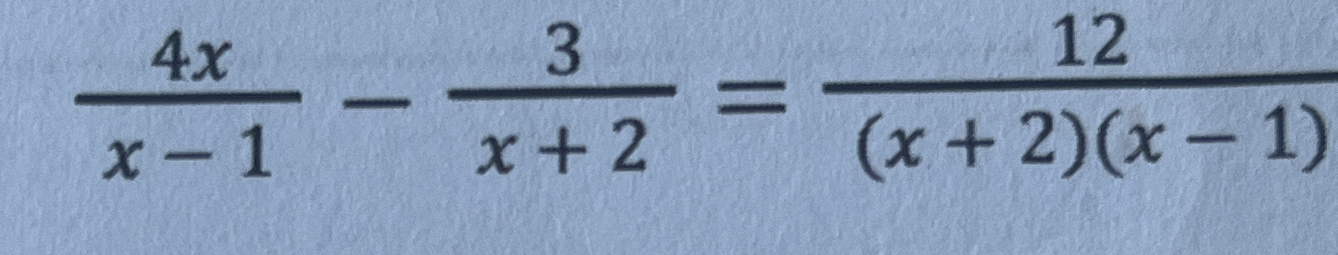
Understand the Problem
The question asks to solve the equation for x. This involves algebraic manipulation to combine terms and isolate x.
Answer
$x = -\frac{9}{4}$
Answer for screen readers
$x = -\frac{9}{4}$
Steps to Solve
- Multiply both sides by $(x+2)(x-1)$
To eliminate the denominators, multiply both sides of the equation by the common denominator $(x+2)(x-1)$.
$$ (x+2)(x-1) \left( \frac{4x}{x-1} - \frac{3}{x+2} \right) = (x+2)(x-1) \left( \frac{12}{(x+2)(x-1)} \right) $$
- Simplify the equation
Distribute $(x+2)(x-1)$ on the left side and cancel out common factors:
$$ 4x(x+2) - 3(x-1) = 12 $$
- Expand and simplify
Expand the terms on the left side
$$ 4x^2 + 8x - 3x + 3 = 12 $$
Combine like terms
$$ 4x^2 + 5x + 3 = 12 $$
- Move constant to the left side
Subtract 12 from both sides to set the equation to zero:
$$ 4x^2 + 5x + 3 - 12 = 0 $$ $$ 4x^2 + 5x - 9 = 0 $$
- Factor the quadratic equation
Factor the quadratic equation $4x^2 + 5x - 9 = 0$
$$ (4x + 9)(x - 1) = 0 $$
- Solve for x
Set each factor equal to zero and solve for $x$: $4x + 9 = 0$ or $x - 1 = 0$
For $4x + 9 = 0$: $4x = -9$ $x = -\frac{9}{4}$
For $x - 1 = 0$: $x = 1$
- Check for extraneous solutions
Check if $x = 1$ and $x = -\frac{9}{4}$ are valid solutions by plugging them back into the original equation. Note that $x=1$ would make the denominator of the first term and the right side equal to zero, so it is an extraneous solution.
If $x = 1$, then $x-1 = 0$, so the first term $\frac{4x}{x-1}$ is undefined. Thus $x=1$ is not a solution.
If $x = -\frac{9}{4}$:
The original equation is: $\frac{4x}{x-1} - \frac{3}{x+2} = \frac{12}{(x+2)(x-1)}$ Substitute $x = -\frac{9}{4}$: $\frac{4(-\frac{9}{4})}{-\frac{9}{4}-1} - \frac{3}{-\frac{9}{4}+2} = \frac{12}{(-\frac{9}{4}+2)(-\frac{9}{4}-1)}$ $\frac{-9}{-\frac{13}{4}} - \frac{3}{-\frac{1}{4}} = \frac{12}{(-\frac{1}{4})(-\frac{13}{4})}$ $\frac{36}{13} + 12 = \frac{12}{\frac{13}{16}}$ $\frac{36}{13} + \frac{156}{13} = \frac{192}{13}$ $\frac{192}{13} = \frac{192}{13}$ Therefore, $x = -\frac{9}{4}$ is a valid solution.
$x = -\frac{9}{4}$
More Information
The solution to the equation is $x = -\frac{9}{4}$. It's important to check for extraneous solutions in rational equations because some solutions obtained algebraically might not satisfy the original equation due to division by zero.
Tips
A common mistake is not checking for extraneous solutions, particularly when dealing with rational equations. In this case, $x=1$ is an extraneous solution because it makes one of the denominators zero. Also, mistakes during factoring and simplification can occur, so it is important to double check your work.
AI-generated content may contain errors. Please verify critical information