Solve for x: 5(1 + 6x) = 3
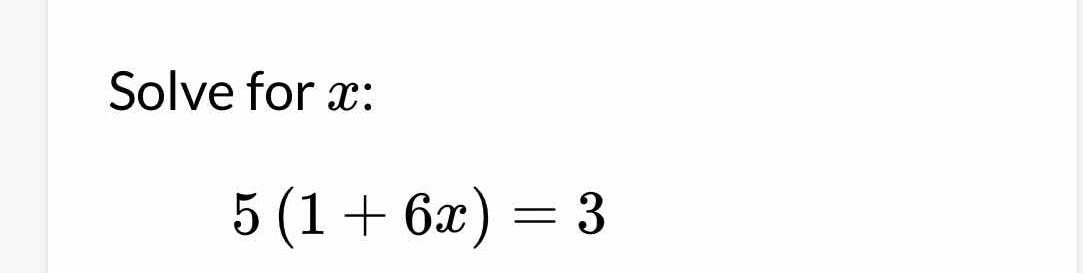
Understand the Problem
The question is asking us to solve the equation (5(1 + 6x) = 3) for the variable (x). We will need to use the distributive property to expand the left side of the equation, then isolate (x) by performing algebraic operations on both sides.
Answer
$x = -\frac{1}{15}$
Answer for screen readers
$x = -\frac{1}{15}$
Steps to Solve
-
Apply the distributive property Distribute the 5 across the terms inside the parentheses: $5(1 + 6x) = 5 \cdot 1 + 5 \cdot 6x = 5 + 30x$ So, the equation becomes $5 + 30x = 3$.
-
Isolate the term with x Subtract 5 from both sides of the equation to isolate the term containing $x$: $5 + 30x - 5 = 3 - 5$ $30x = -2$
-
Solve for x Divide both sides by 30 to solve for $x$: $\frac{30x}{30} = \frac{-2}{30}$ $x = -\frac{2}{30}$
-
Simplify the fraction Simplify the fraction by dividing both the numerator and denominator by their greatest common divisor, which is 2: $x = -\frac{2 \div 2}{30 \div 2}$ $x = -\frac{1}{15}$
$x = -\frac{1}{15}$
More Information
The solution to the equation $5(1 + 6x) = 3$ is $x = -\frac{1}{15}$. This means that if you substitute $-\frac{1}{15}$ for $x$ in the original equation, the equation will be true.
Tips
A common mistake is not distributing the 5 correctly across both terms inside the parentheses. It is important to multiply both the 1 and the 6x by 5. Another common mistake is making errors when adding or subtracting on both sides of the equation. You need to make sure you perform the same operation on both sides to maintain equality. Lastly, forgetting to simplify the final fraction is another common error.
AI-generated content may contain errors. Please verify critical information