Solve for x: $4x^2 + 10 = 11$
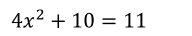
Understand the Problem
The question asks to solve the equation $4x^2 + 10 = 11$ for the variable $x$. This involves algebraic manipulation to isolate $x$ and find its value(s).
Answer
$x = \pm \frac{1}{2}$
Answer for screen readers
$x = \frac{1}{2}$ and $x = -\frac{1}{2}$
Steps to Solve
- Isolate the $x^2$ term
Subtract 10 from both sides of the equation:
$4x^2 + 10 - 10 = 11 - 10$
This simplifies to:
$4x^2 = 1$
- Divide to isolate $x^2$
Divide both sides of the equation by 4:
$\frac{4x^2}{4} = \frac{1}{4}$
This simplifies to:
$x^2 = \frac{1}{4}$
- Take the square root of both sides
Take the square root of both sides of the equation to solve for $x$:
$\sqrt{x^2} = \sqrt{\frac{1}{4}}$
Remember to consider both the positive and negative square roots:
$x = \pm \frac{1}{2}$
$x = \frac{1}{2}$ and $x = -\frac{1}{2}$
More Information
When solving an equation of the form $x^2 = a$, there are generally two solutions: $x = \sqrt{a}$ and $x = -\sqrt{a}$. This is because both $(\sqrt{a})^2$ and $(-\sqrt{a})^2$ equal $a$.
Tips
A common mistake is forgetting to include both the positive and negative square roots when solving for $x$. Always remember that when you take the square root of both sides of an equation, you must consider both positive and negative solutions.
AI-generated content may contain errors. Please verify critical information