Solve for x: 3/(x^2+5x+6) + (x-1)/(x+2) = 7/(x+3)
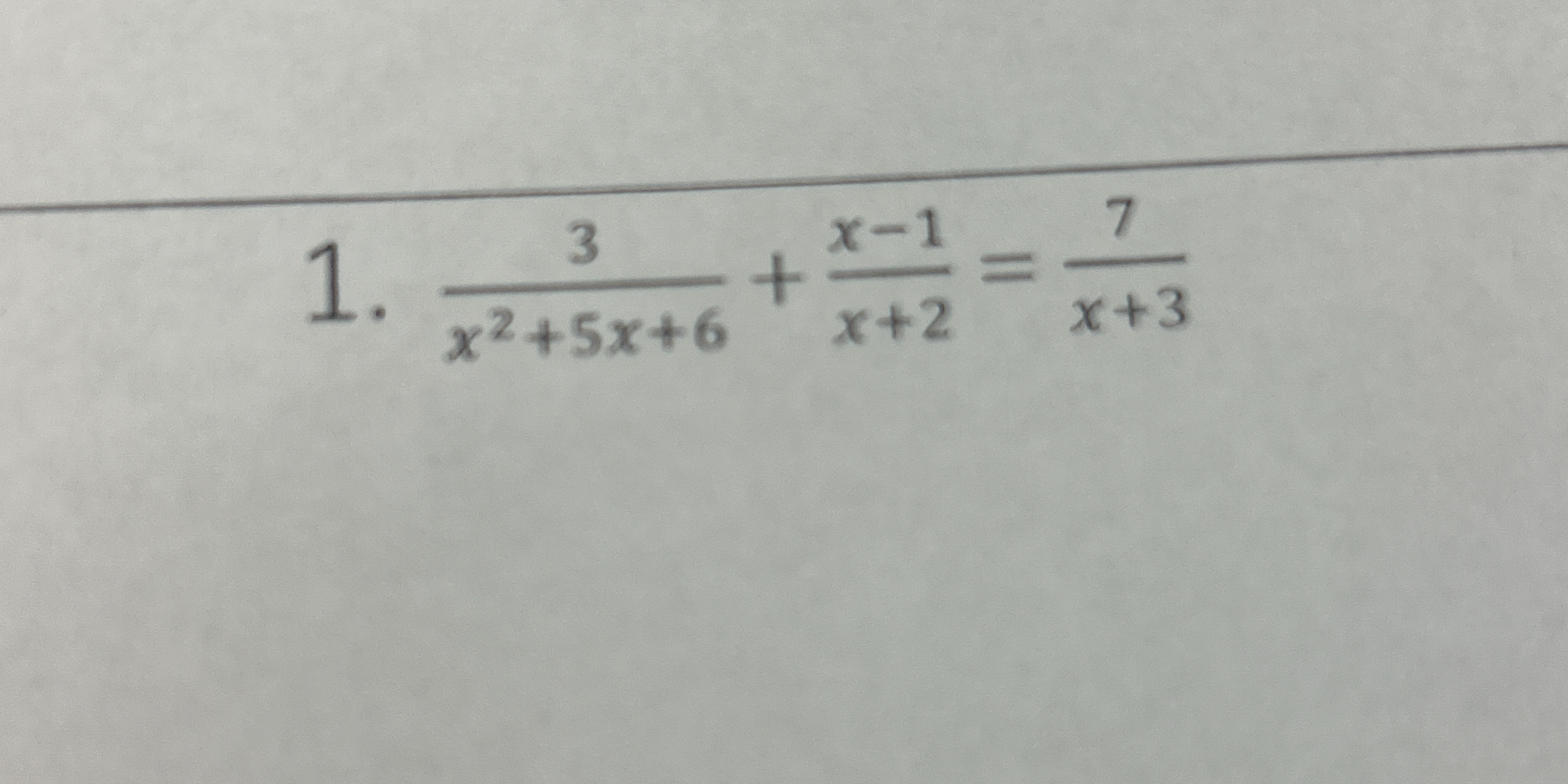
Understand the Problem
The question asks us to solve the algebraic equation for x. We need to isolate x through multiple algebraic manipulations such as factoring, finding common denominators, combining like terms, and potentially using the quadratic formula.
Answer
$x = 7$
Answer for screen readers
$x = 7$
Steps to Solve
- Factor the quadratic
Factor the quadratic in the denominator of the first term: $x^2 + 5x + 6 = (x+2)(x+3)$ The equation then becomes: $$ \frac{3}{(x+2)(x+3)} + \frac{x-1}{x+2} = \frac{7}{x+3} $$
- Find a common denominator
The common denominator is $(x+2)(x+3)$. Multiply each term by the appropriate factor to achieve this common denominator. $$ \frac{3}{(x+2)(x+3)} + \frac{(x-1)(x+3)}{(x+2)(x+3)} = \frac{7(x+2)}{(x+3)(x+2)} $$
- Combine the fractions
Since the denominators are the same, we can combine the numerators: $$ \frac{3 + (x-1)(x+3)}{(x+2)(x+3)} = \frac{7(x+2)}{(x+3)(x+2)} $$
- Eliminate the denominators
Since both sides of the equation have the same denominator, we can equate the numerators: $$ 3 + (x-1)(x+3) = 7(x+2) $$
- Expand and simplify
Expand the products: $$ 3 + (x^2 + 3x - x - 3) = 7x + 14 $$ $$ 3 + x^2 + 2x - 3 = 7x + 14 $$ $$ x^2 + 2x = 7x + 14 $$
- Rearrange into a quadratic equation
Move all terms to one side to set the equation to zero: $$ x^2 + 2x - 7x - 14 = 0 $$ $$ x^2 - 5x - 14 = 0 $$
- Factor the quadratic equation
Factor the quadratic: $$ (x - 7)(x + 2) = 0 $$
- Solve for x
Set each factor equal to zero and solve for $x$: $$ x - 7 = 0 \implies x = 7 $$ $$ x + 2 = 0 \implies x = -2 $$
- Check for extraneous solutions
We must check if any of the solutions make the original denominators equal to zero. If $x = -2$, the denominators $x+2$ and $x^2+5x+6 = (x+2)(x+3)$ would be zero, so $x = -2$ is an extraneous solution. If $x = 7$, none of the denominators are zero, so $x = 7$ is a valid solution.
$x = 7$
More Information
The solution to the equation is $x = 7$. Note that $x = -2$ is an extraneous solution because it makes the denominator of some terms in the original equation equal to zero, which is undefined.
Tips
A common mistake is forgetting to check for extraneous solutions. When solving equations with rational expressions, it is crucial to substitute the solutions back into the original equation to ensure that no denominators are equal to zero. Failing to do so can lead to including extraneous solutions, which are not valid. Another common mistake is an error in factoring the quadratic equation.
AI-generated content may contain errors. Please verify critical information