Solve for x: $3^{x+1} = 3^{x-1} + 2^3$
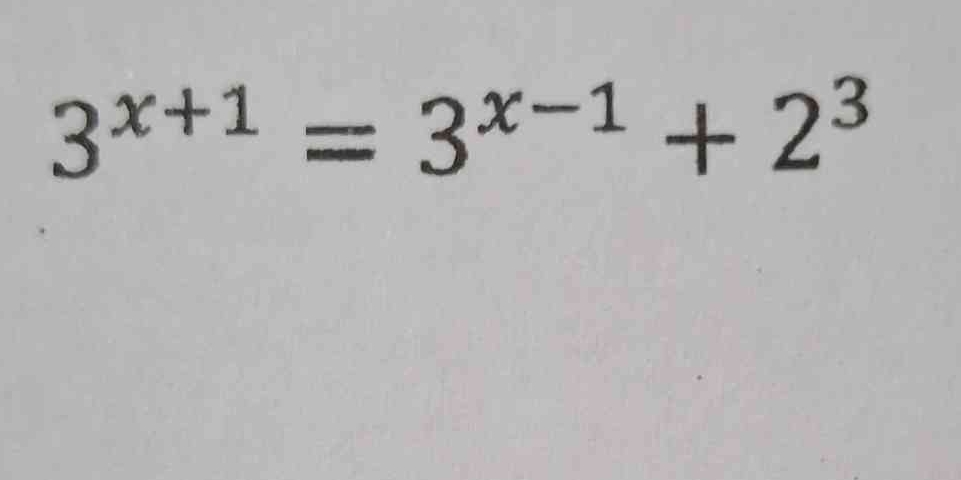
Understand the Problem
The question asks to solve for x in the exponential equation $3^{x+1} = 3^{x-1} + 2^3$. We will solve it by simplifying the equation and isolating x.
Answer
$x = 1$
Answer for screen readers
$x = 1$
Steps to Solve
-
Rewrite the equation Rewrite the equation $3^{x+1} = 3^{x-1} + 2^3$.
-
Simplify $2^3$ $2^3 = 8$, so the equation becomes $3^{x+1} = 3^{x-1} + 8$.
-
Rewrite $3^{x+1}$ and $3^{x-1}$ using exponent rules Using the rule $a^{m+n} = a^m \cdot a^n$, we can rewrite $3^{x+1}$ as $3^x \cdot 3^1 = 3 \cdot 3^x$ and $3^{x-1}$ as $3^x \cdot 3^{-1} = \frac{3^x}{3}$. The original equation can be rewritten as: $3 \cdot 3^x = \frac{3^x}{3} + 8$
-
Multiply both sides by 3 To eliminate the fraction, multiply both sides of the equation by 3: $3(3 \cdot 3^x) = 3(\frac{3^x}{3} + 8)$ which simplifies to $9 \cdot 3^x = 3^x + 24$
-
Isolate the terms with $3^x$ Subtract $3^x$ from both sides: $9 \cdot 3^x - 3^x = 24$, which simplifies to $8 \cdot 3^x = 24$
-
Isolate $3^x$ Divide both sides by 8: $3^x = \frac{24}{8}$, which simplifies to $3^x = 3$
-
Solve for x Since $3^x = 3$, and $3 = 3^1$, we have $3^x = 3^1$. Therefore, $x = 1$.
$x = 1$
More Information
The value of x that satisfies the equation $3^{x+1} = 3^{x-1} + 2^3$ is 1.
Tips
A common mistake is incorrectly applying the exponent rules when simplifying $3^{x+1}$ and $3^{x-1}$. Another mistake is not properly distributing when multiplying both sides of the equation by 3.
AI-generated content may contain errors. Please verify critical information