Solve for x: $2x^2 - x = 10$
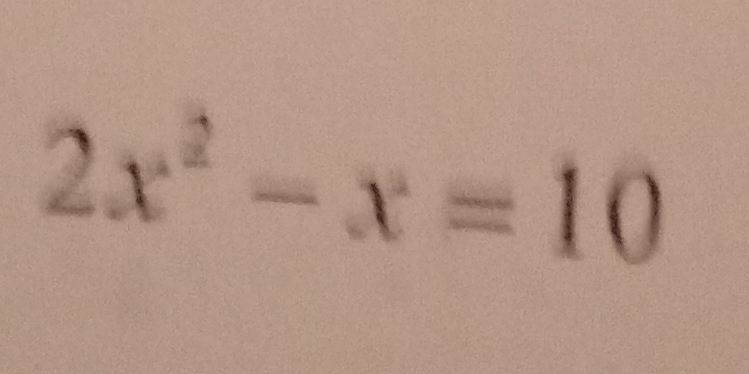
Understand the Problem
The question requires solving the quadratic equation $2x^2 - x = 10$ for the variable x. To do this, we must first rearrange the equation into standard quadratic form, which is $ax^2 + bx + c = 0$, and then we can use the quadratic formula or factoring to find the values of x that satisfy the equation.
Answer
$x = \frac{5}{2}, -2$
Answer for screen readers
$x = \frac{5}{2}, -2$
Steps to Solve
-
Rewrite the equation in standard form Subtract 10 from both sides of the equation to set it equal to zero. $2x^2 - x - 10 = 0$
-
Identify the coefficients In the standard quadratic equation $ax^2 + bx + c = 0$, identify the values of $a$, $b$, and $c$. $a = 2$, $b = -1$, $c = -10$
-
Apply the quadratic formula Use the quadratic formula to solve for x: $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$
-
Substitute the values Substitute the values of a, b, and c into the quadratic formula: $$x = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(2)(-10)}}{2(2)}$$
-
Simplify the expression Simplify the expression to find the values of x. $$x = \frac{1 \pm \sqrt{1 + 80}}{4}$$ $$x = \frac{1 \pm \sqrt{81}}{4}$$ $$x = \frac{1 \pm 9}{4}$$
-
Calculate the two possible values of x Calculate the two possible values of x: $$x_1 = \frac{1 + 9}{4} = \frac{10}{4} = \frac{5}{2}$$ $$x_2 = \frac{1 - 9}{4} = \frac{-8}{4} = -2$$
$x = \frac{5}{2}, -2$
More Information
The solutions to the quadratic equation $2x^2 - x = 10$ are $x = \frac{5}{2}$ and $x = -2$. These are the x-intercepts of the quadratic function $f(x) = 2x^2 - x - 10$.
Tips
A common mistake is to incorrectly identify the coefficients a, b, and c or to make errors when substituting them into the quadratic formula. Another common mistake is making arithmetic errors when simplifying the expression after substituting the coefficients.
AI-generated content may contain errors. Please verify critical information