Solve for x: 0 = 4x^3 - 24x^2 + 12x + 40
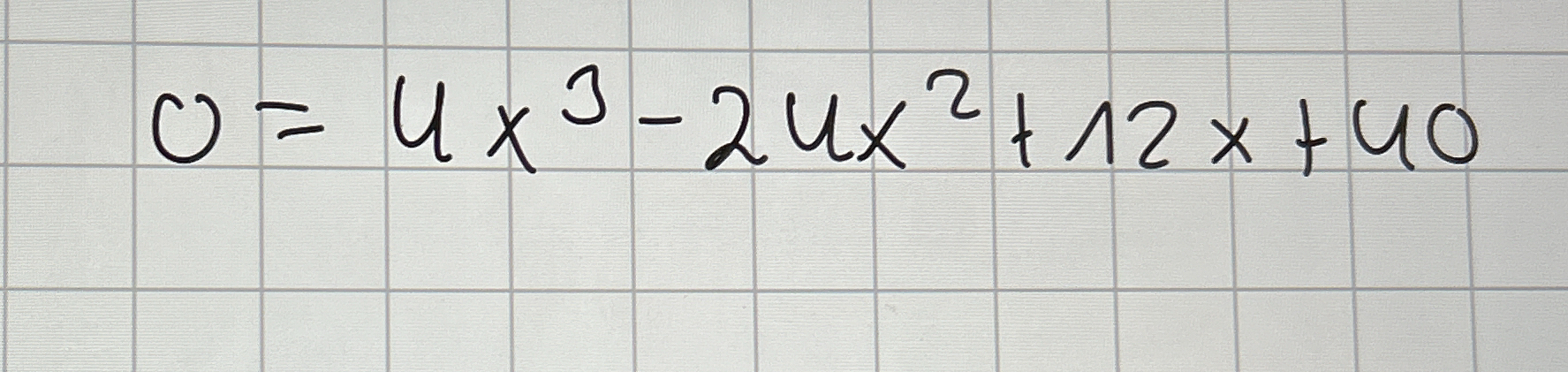
Understand the Problem
The question asks to find the roots of the given cubic equation. This involves finding the values of x that satisfy the equation. Factoring or numerical methods may be required to find the roots.
Answer
$x = -1, 2, 5$
Answer for screen readers
$x = -1, 2, 5$
Steps to Solve
- Simplify the equation
Divide the entire equation by 4 to simplify it: $$ \frac{4x^3}{4} - \frac{24x^2}{4} + \frac{12x}{4} + \frac{40}{4} = \frac{0}{4} $$ This simplifies to: $$ x^3 - 6x^2 + 3x + 10 = 0 $$
- Find a root by testing factors of the constant term
The constant term is 10. We need to find a factor of 10 that, when substituted for $x$, makes the equation equal to zero. Factors of 10 include $\pm1, \pm2, \pm5, \pm10$. Test $x = -1$: $$ (-1)^3 - 6(-1)^2 + 3(-1) + 10 = -1 - 6 - 3 + 10 = 0$$ So, $x = -1$ is a root.
- Perform synthetic division
Since $x = -1$ is a root, $(x + 1)$ is a factor. Use synthetic division to divide the polynomial $x^3 - 6x^2 + 3x + 10$ by $(x + 1)$.
-1 | 1 -6 3 10
| -1 7 -10
-------------------
1 -7 10 0
This gives us the quotient $x^2 - 7x + 10$.
- Factor the quadratic equation
Now, factor the quadratic equation $x^2 - 7x + 10 = 0$. We are looking for two numbers that multiply to 10 and add up to -7. These numbers are -2 and -5. So, the quadratic equation factors to: $$ (x - 2)(x - 5) = 0$$
- Solve for the remaining roots
Set each factor equal to zero and solve for $x$: $$ x - 2 = 0 \implies x = 2$$ $$ x - 5 = 0 \implies x = 5$$
- List all roots
The roots of the original equation are $x = -1, 2, 5$.
$x = -1, 2, 5$
More Information
Cubic equations can have up to three real roots. In this case, we found three distinct real roots.
Tips
- Not simplifying the equation first, which makes factoring harder.
- Incorrectly applying synthetic division, leading to a wrong quadratic equation.
- Making errors when factoring the quadratic equation.
- Forgetting to test negative factors when looking for a root.
AI-generated content may contain errors. Please verify critical information