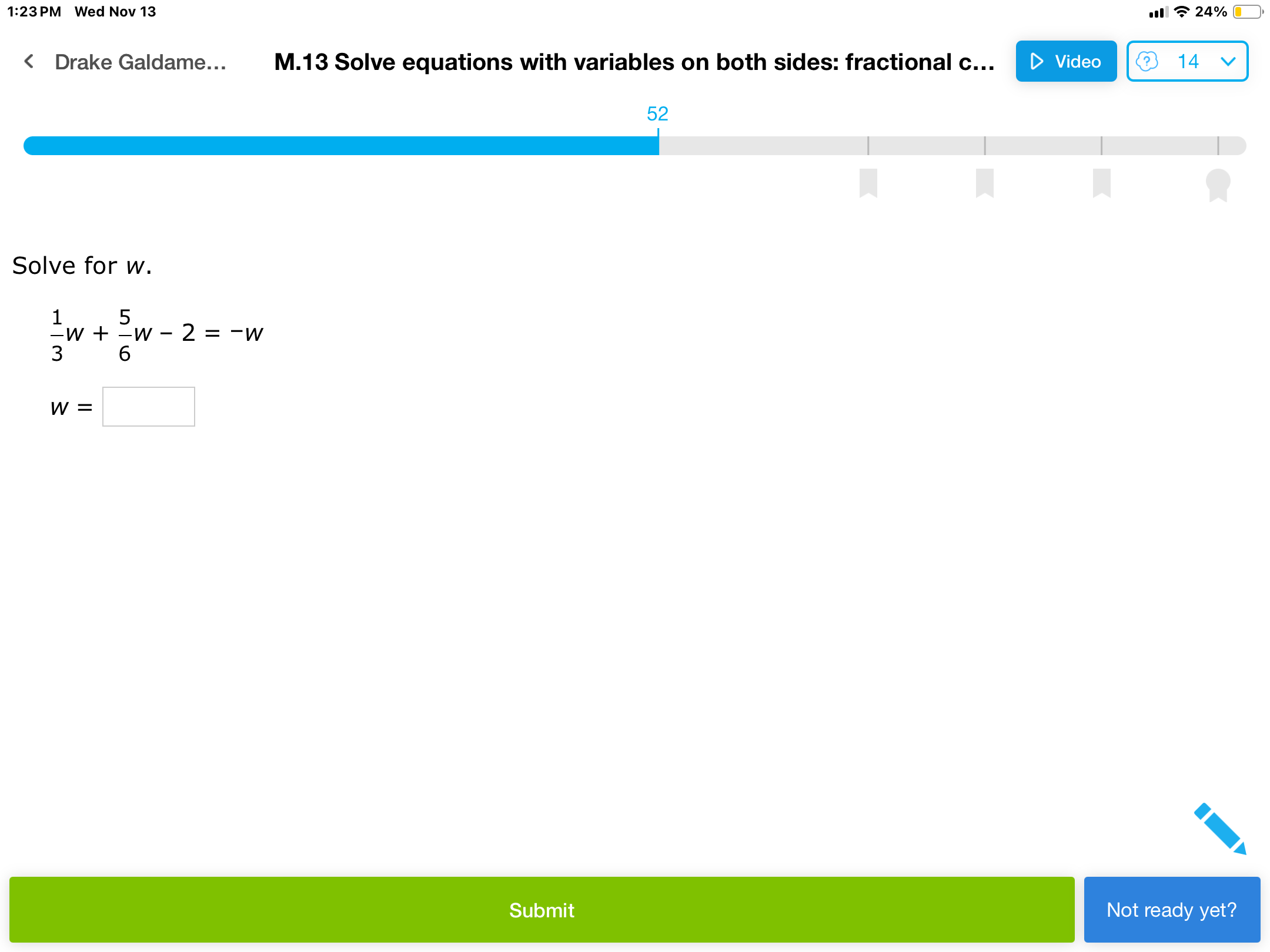
Solve for w. \frac{-w}{3} + \frac{5w}{6} - 2 = -w
Understand the Problem
The question is asking to solve the equation for the variable w. It includes fractions and multiple terms involving w, which will require algebraic manipulation to isolate w on one side of the equation.
Answer
The value of \( w \) is \( \frac{4}{3} \).
Answer for screen readers
The value of ( w ) is ( \frac{4}{3} ).
Steps to Solve
- Combine like terms First, let's rewrite the equation clearly: $$ \frac{-w}{3} + \frac{5w}{6} - 2 = -w. $$
To eliminate fractions, find the least common denominator (LCD), which is 6. Multiply every term by 6: $$ 6 \left( \frac{-w}{3} \right) + 6 \left( \frac{5w}{6} \right) - 6 \times 2 = 6 \times (-w). $$
This simplifies to: $$ -2w + 5w - 12 = -6w. $$
-
Simplify the equation Now, combine like terms on the left side: $$ 3w - 12 = -6w. $$
-
Isolate the variable w Next, add $6w$ to both sides to move all terms involving $w$ to one side: $$ 3w + 6w - 12 = 0. $$
This simplifies to: $$ 9w - 12 = 0. $$
- Solve for w Now, add 12 to both sides: $$ 9w = 12. $$
Finally, divide by 9: $$ w = \frac{12}{9}. $$
- Simplify the fraction Simplifying gives: $$ w = \frac{4}{3}. $$
The value of ( w ) is ( \frac{4}{3} ).
More Information
The solution to the equation ( \frac{-w}{3} + \frac{5w}{6} - 2 = -w ) requires manipulating fractions by eliminating the denominators. The process includes isolating the variable on one side and simplifies the equation.
Tips
- Not finding the common denominator: Ensure you identify the least common denominator to clear fractions effectively.
- Combining terms incorrectly: Be cautious when adding or subtracting coefficients of ( w ).
AI-generated content may contain errors. Please verify critical information