Solve for n: 2^(-n) = (1/2)^3
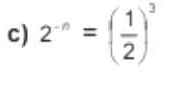
Understand the Problem
The question asks to solve for the unknown variable 'n' in the exponential equation provided. This involves understanding exponent rules and algebraic manipulation to isolate 'n'.
Answer
$n=3$
Answer for screen readers
$n=3$
Steps to Solve
- Rewrite the right side of the equation using exponent rules
We can rewrite $(\frac{1}{2})^3$ as $2^{-3}$ because $\frac{1}{2} = 2^{-1}$, so $(\frac{1}{2})^3 = (2^{-1})^3 = 2^{-3}$.
The equation becomes: $2^{-n} = 2^{-3}$
- Equate the exponents
Since the bases are equal, we can set the exponents equal to each other: $-n = -3$
- Solve for n
Multiply or divide both sides of the equation by -1: $n = 3$
$n=3$
More Information
The value of $n$ that satisfies the equation $2^{-n} = (\frac{1}{2})^3$ is 3.
Tips
A common mistake is forgetting the negative sign when equating the exponents, which would lead to an incorrect answer of $n = -3$.
AI-generated content may contain errors. Please verify critical information