Solve for c: \frac{1}{2}c = -3 - \frac{3}{2} - \frac{5}{2}c + 1
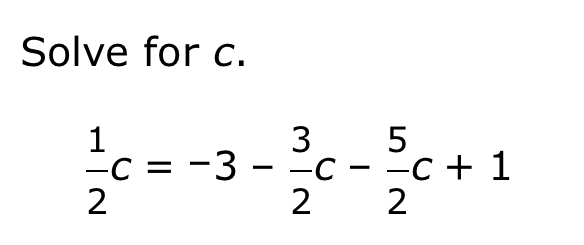
Understand the Problem
The question is asking to solve the equation for the variable c. This involves isolating c on one side of the equation and simplifying the expression accordingly.
Answer
The value of \( c \) is \( -\frac{7}{6} \).
Answer for screen readers
The solution for ( c ) is
$$ c = -\frac{7}{6} $$
Steps to Solve
- Combine Like Terms on the Right Side
Start by simplifying the right side of the equation:
$$ -3 - \frac{3}{2} + 1 = -3 + 1 - \frac{3}{2} = -2 - \frac{3}{2} $$
Convert -2 to a fraction:
$$ -2 = -\frac{4}{2} $$
So,
$$ -2 - \frac{3}{2} = -\frac{4}{2} - \frac{3}{2} = -\frac{7}{2} $$
Now the equation becomes:
$$ \frac{1}{2}c = -\frac{7}{2} - \frac{5}{2}c $$
- Isolate All Terms Involving c
Move all terms involving $c$ to one side. Add $\frac{5}{2}c$ to both sides:
$$ \frac{1}{2}c + \frac{5}{2}c = -\frac{7}{2} $$
- Combine the Terms Involving c
Combine the $c$ terms:
$$ \frac{1}{2}c + \frac{5}{2}c = \frac{1 + 5}{2}c = \frac{6}{2}c = 3c $$
Now we have:
$$ 3c = -\frac{7}{2} $$
- Solve for c
Divide both sides by 3:
$$ c = -\frac{7}{2} \cdot \frac{1}{3} = -\frac{7}{6} $$
The solution for ( c ) is
$$ c = -\frac{7}{6} $$
More Information
This result shows that ( c ) is a negative fraction, which can occur in linear equations. Understanding the manipulation of terms is key to solving for a variable.
Tips
- Failing to combine like terms properly can lead to incorrect simplifications.
- Neglecting to distribute negative signs when moving terms across the equation can result in errors. Always check that signs are maintained.
AI-generated content may contain errors. Please verify critical information