Solve for c: 1/c = -3 - 3/2 - c - 5/2 - c + 1
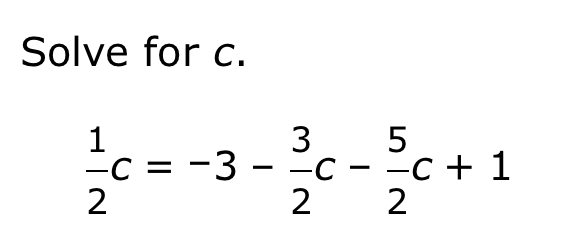
Understand the Problem
The question is asking us to solve the equation for the variable c. It presents a rational function and several linear terms involving c. To solve it, we will first simplify both sides of the equation, combine like terms, and isolate c.
Answer
The solutions for \(c\) are \( c = \frac{-3 + \sqrt{7}}{2} \) and \( c = \frac{-3 - \sqrt{7}}{2} \).
Answer for screen readers
The solutions for (c) are:
$$ c = \frac{-3 + \sqrt{7}}{2} \quad \text{and} \quad c = \frac{-3 - \sqrt{7}}{2} $$
Steps to Solve
- Start with the original equation
We begin with the equation:
$$\frac{1}{c} = -3 - \frac{3}{2} - c - \frac{5}{2} - c + 1$$
- Simplify the right side
Combine the constant terms on the right side:
- Combine $-3$, $-\frac{3}{2}$, and $-\frac{5}{2}$.
$$ -3 = -\frac{6}{2} \quad (3 = \frac{6}{2})$$
So,
$$ -3 - \frac{3}{2} - \frac{5}{2} = -\frac{6}{2} - \frac{3}{2} - \frac{5}{2} = -\frac{14}{2} = -7 $$
Now substitute back:
$$\frac{1}{c} = -7 - 2c + 1$$
Combine constants on the right:
$$ -7 + 1 = -6 $$
So now we have:
$$\frac{1}{c} = -6 - 2c$$
- Clear the fraction
Multiply both sides by $c$ to eliminate the fraction (assuming $c \neq 0$):
$$1 = c(-6 - 2c)$$
Which simplifies to:
$$1 = -6c - 2c^2$$
- Rearrange into standard quadratic form
Rearranging gives us the equation:
$$2c^2 + 6c + 1 = 0$$
- Apply the quadratic formula
To find the values of $c$, we'll use the quadratic formula:
$$c = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$
Where (a = 2), (b = 6), and (c = 1).
Calculating the discriminant:
$$b^2 - 4ac = 6^2 - 4(2)(1) = 36 - 8 = 28$$
Now apply the quadratic formula:
$$c = \frac{-6 \pm \sqrt{28}}{4} = \frac{-6 \pm 2\sqrt{7}}{4} = \frac{-3 \pm \sqrt{7}}{2}$$
The solutions for (c) are:
$$ c = \frac{-3 + \sqrt{7}}{2} \quad \text{and} \quad c = \frac{-3 - \sqrt{7}}{2} $$
More Information
The equation started as a rational function that eventually led to finding the roots of a quadratic equation. Quadratic formulas provide two potential solutions, showing the nature of the solutions.
Tips
- Forgetting to combine like terms properly, which can lead to incorrect coefficients in the quadratic equation.
- Not applying the quadratic formula correctly, especially miscalculating the discriminant.
AI-generated content may contain errors. Please verify critical information