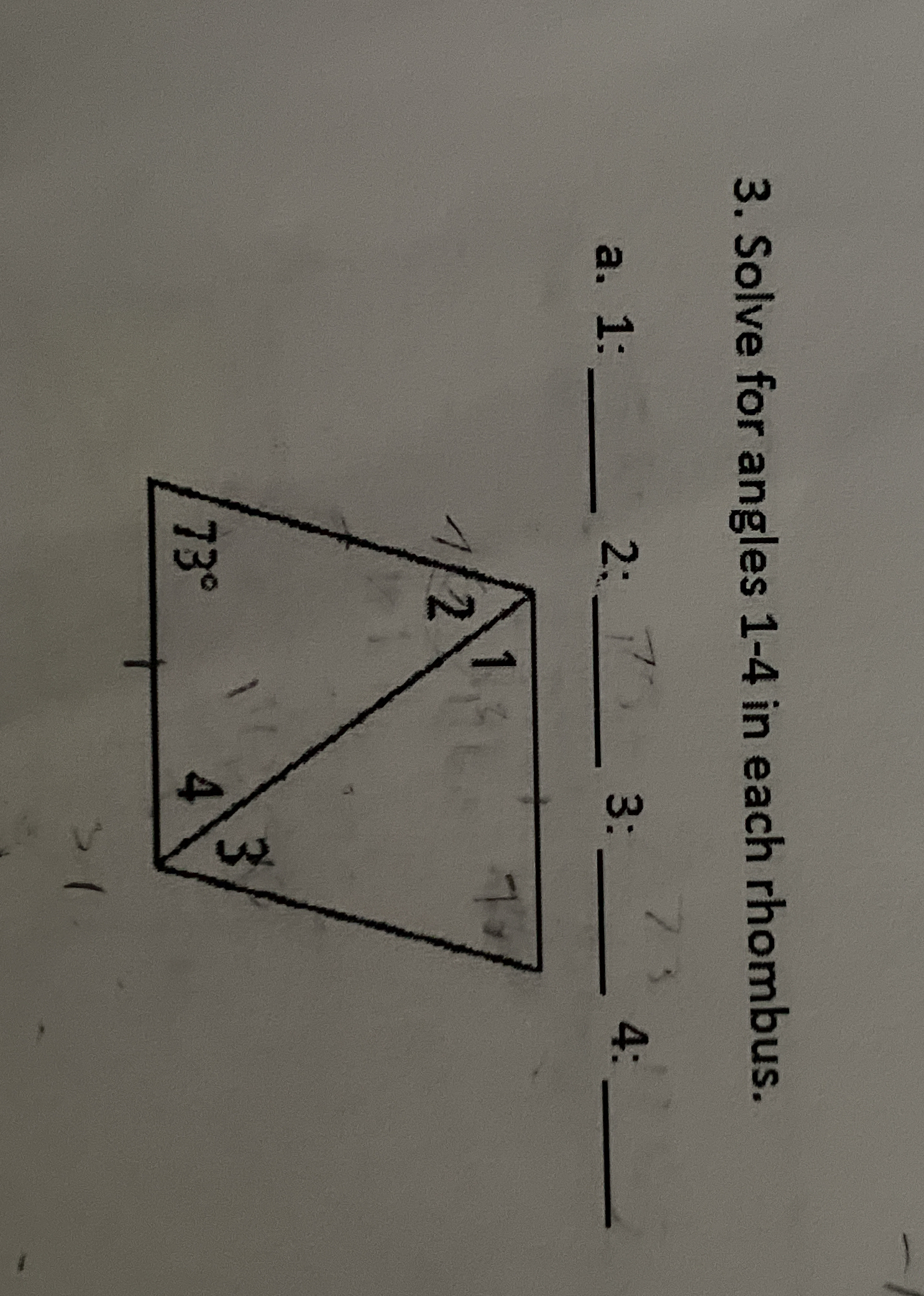
Solve for angles 1-4 in each rhombus.
Understand the Problem
The question is asking to solve for the four angles in a rhombus, given that one angle measures 73 degrees. This involves using properties of a rhombus, where opposite angles are equal, and adjacent angles are supplementary.
Answer
Angle 1: $73^\circ$, Angle 2: $107^\circ$, Angle 3: $73^\circ$, Angle 4: $107^\circ$
Answer for screen readers
Angle 1: $73^\circ$
Angle 2: $107^\circ$
Angle 3: $73^\circ$
Angle 4: $107^\circ$
Steps to Solve
-
Identify Given Angle The first angle, angle 1, is given as $73^\circ$.
-
Find Opposite Angle In a rhombus, opposite angles are equal. Therefore, angle 3 is also $73^\circ$. $$ \text{Angle 3} = 73^\circ $$
-
Find Adjacent Angles Adjacent angles in a rhombus are supplementary. Thus, the sum of angle 1 and angle 2 is $180^\circ$. $$ \text{Angle 1} + \text{Angle 2} = 180^\circ $$ Substituting in the known value: $$ 73^\circ + \text{Angle 2} = 180^\circ $$
-
Solve for Angle 2 Rearranging the equation gives: $$ \text{Angle 2} = 180^\circ - 73^\circ $$ Calculating this provides: $$ \text{Angle 2} = 107^\circ $$
-
Find Opposite Angle 4 Again, since opposite angles are equal, angle 4 will also be $107^\circ$. $$ \text{Angle 4} = 107^\circ $$
Angle 1: $73^\circ$
Angle 2: $107^\circ$
Angle 3: $73^\circ$
Angle 4: $107^\circ$
More Information
In a rhombus, the properties of angles play a crucial role. Opposite angles are equal, and adjacent angles always add up to $180^\circ$. This problem illustrates the use of these properties in finding all angle measures when one is given.
Tips
- Confusing opposite angles with adjacent angles, leading to incorrect assumptions about their measures.
- Forgetting that adjacent angles in a rhombus sum to $180^\circ$.
AI-generated content may contain errors. Please verify critical information