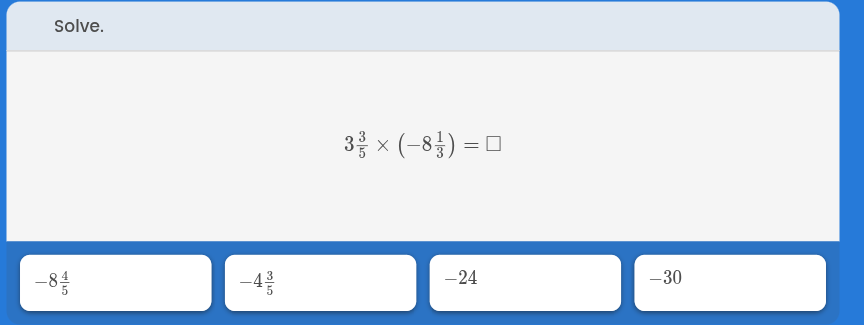
Solve: 3 3/5 * (-8 1/3) = ?
Understand the Problem
The question requires solving a multiplication problem involving mixed numbers. We first need to convert the mixed numbers into improper fractions. Then, multiply the fractions and simplify the result.
Answer
$-30$
Answer for screen readers
$-30$
Steps to Solve
- Convert the mixed numbers to improper fractions
To convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator. Then, place the result over the original denominator.
$3\frac{3}{5} = \frac{(3 \times 5) + 3}{5} = \frac{15+3}{5} = \frac{18}{5}$
$-8\frac{1}{3} = -\frac{(8 \times 3) + 1}{3} = -\frac{24+1}{3} = -\frac{25}{3}$
- Multiply the improper fractions
$\frac{18}{5} \times (-\frac{25}{3}) = -\frac{18 \times 25}{5 \times 3}$
- Simplify the fraction before multiplying
Divide 18 by 3 and 25 by 5
$-\frac{18 \times 25}{5 \times 3} = -\frac{6 \times 5}{1 \times 1}$
- Perform the multiplication
$-\frac{6 \times 5}{1 \times 1} = -\frac{30}{1} = -30$
$-30$
More Information
The product of $3\frac{3}{5}$ and $-8\frac{1}{3}$ is $-30$.
Tips
A common mistake is forgetting to apply the negative sign when dealing with negative numbers.
AI-generated content may contain errors. Please verify critical information