Solve: 2^{x+1} * 2^{3y+1} = 8 and 2^{x+2} * 2^{2y+2} = 16
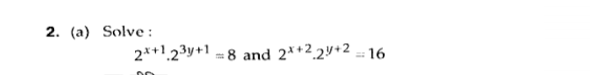
Understand the Problem
The question is asking to solve a system of equations given two equations involving terms of the variables x and y. The equations involve exponents and constants, indicating a potential application of algebraic methods to find values for x and y.
Answer
$x = -2$, $y = 1$
Answer for screen readers
The solution to the system of equations is $x = -2$ and $y = 1$.
Steps to Solve
- Rewrite the equations using properties of exponents
Since $8 = 2^3$ and $16 = 2^4$, we can rewrite the equations as:
- The first equation: $$ 2^{x+1} \cdot 2^{3y+1} = 2^3 $$
- The second equation: $$ 2^{x+2} \cdot 2^{2y+2} = 2^4 $$
- Combine the exponents
Using the property of exponents that states $a^m \cdot a^n = a^{m+n}$, we can combine the left-hand sides:
-
For the first equation: $$ 2^{(x+1)+(3y+1)} = 2^3 $$ This simplifies to: $$ 2^{x + 3y + 2} = 2^3 $$
-
For the second equation: $$ 2^{(x+2)+(2y+2)} = 2^4 $$ This simplifies to: $$ 2^{x + 2y + 4} = 2^4 $$
- Set the exponents equal
Since the bases are equal, we can set the exponents equal to each other:
- From the first equation: $$ x + 3y + 2 = 3 $$
- From the second equation: $$ x + 2y + 4 = 4 $$
- Solve for one variable from one equation
From the first equation, isolate $x$: $$ x = 3 - 3y - 2 $$ $$ x = 1 - 3y $$
- Substitute into the second equation
Now substitute for $x$ in the second equation: $$ (1 - 3y) + 2y + 4 = 4 $$
- Simplify and solve for $y$
Combine like terms: $$ 1 - 3y + 2y + 4 = 4 $$ This simplifies to: $$ 5 - y = 4 $$ Isolating $y$ gives: $$ -y = 4 - 5 $$ $$ -y = -1 $$ $$ y = 1 $$
- Use the value of $y$ to find $x$
Now substitute $y = 1$ back into the expression for $x$: $$ x = 1 - 3(1) $$ $$ x = 1 - 3 $$ $$ x = -2 $$
The solution to the system of equations is $x = -2$ and $y = 1$.
More Information
This system of equations involves applying properties of exponents, allowing you to simplify and solve for the variables systematically. Recognizing base equivalencies is key for solving exponential equations.
Tips
- Ignoring the properties of exponents: Make sure to use $a^m \cdot a^n = a^{m+n}$ correctly.
- Mixing up the solution steps: Ensure to isolate the variables correctly before substituting values to avoid confusion.
AI-generated content may contain errors. Please verify critical information