Sketch the region of integration for the integral ∫ from 0 to 2 ∫ from x^2 to 2x (4x + 2) dy dx and write an equivalent integral with the order of integration reversed.
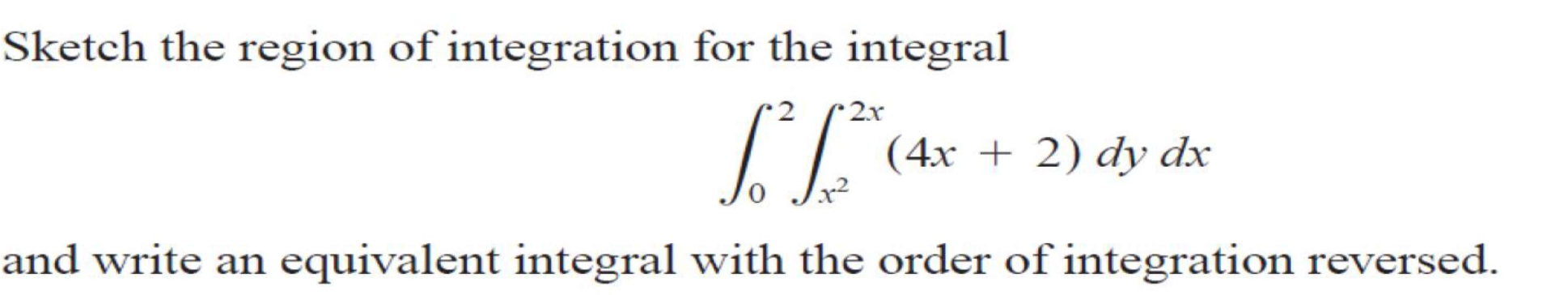
Understand the Problem
The question asks for a sketch of the region of integration defined by the given integral and requires writing an equivalent integral with the order of integration reversed. The integral involves the limits for x and y based on the specified functions.
Answer
$$ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) \, dx \, dy $$
Answer for screen readers
The equivalent integral with the order of integration reversed is: $$ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) , dx , dy $$
Steps to Solve
-
Identify the Limits of Integration
The given integral is ( \int_{0}^{2} \int_{x^2}^{2x} (4x + 2) , dy , dx ). Here, the outer integral has limits ( x = 0 ) to ( x = 2 ), and for each ( x ), the inner integral has limits ( y = x^2 ) to ( y = 2x ).
-
Sketch the Region of Integration
To sketch the region, plot the curves defined by:
-
( y = x^2 ) (a parabola opening upwards)
-
( y = 2x ) (a straight line)
-
The lines ( x = 0 ) and ( x = 2 ) are vertical lines.
The area of integration is bounded below by the parabola ( y = x^2 ) and above by the line ( y = 2x ) between ( x = 0 ) and ( x = 2 ).
-
-
Find Points of Intersection
To find where ( y = x^2 ) intersects ( y = 2x ): Set ( x^2 = 2x ) [ x^2 - 2x = 0 \Rightarrow x(x - 2) = 0 ] So, ( x = 0 ) and ( x = 2 ).
Evaluating ( y ) gives:
- At ( x = 0 ), ( y = 0^2 = 0 )
- At ( x = 2 ), ( y = 2^2 = 4 ) Thus, the intersection points are ( (0, 0) ) and ( (2, 4) ).
-
Write the Reversed Integral
In the reversed order, we need to express ( x ) as a function of ( y ).
From the equations:
- For ( y = x^2 ), we have ( x = \sqrt{y} )
- For ( y = 2x ), we have ( x = \frac{y}{2} )
The limits for ( y ) range from 0 to 4.
Thus, the integral becomes: [ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) , dx , dy ]
The equivalent integral with the order of integration reversed is: $$ \int_{0}^{4} \int_{\sqrt{y}}^{\frac{y}{2}} (4x + 2) , dx , dy $$
More Information
This integral visually represents the same area of integration in the ( xy )-coordinate system. The sketch helps to clarify the region bounded by the curves and the defined limits.
Tips
- Incorrect Limit Interpretation: Ensure that the limits of integration correctly reflect the bounds based on the curve intersections.
- Misidentifying the Area of Integration: Make sure to thoroughly sketch the region to avoid errors in setting up the reversed integral.
AI-generated content may contain errors. Please verify critical information