sin(x) + sin(x)cot(x)^2 = sec(x). Determine the defined range.
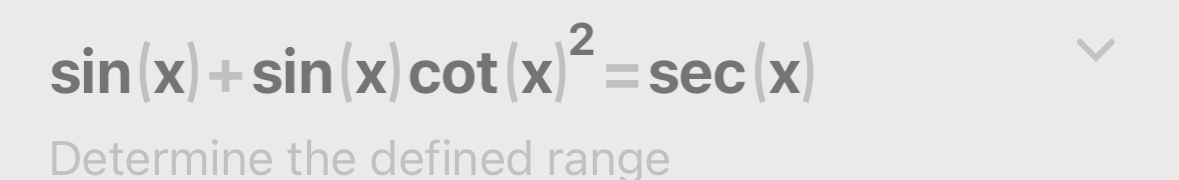
Understand the Problem
The question is asking to determine the defined range for the equation involving trigonometric functions. The approach will involve analyzing the given equation and understanding the properties of the functions involved.
Answer
The defined range for $x$ is where $-1 \leq \cos(x) \leq \frac{1}{\sqrt[3]{4}}$.
Answer for screen readers
The defined range for $x$ satisfying the equation is: $$ x \in { \text{all } x \text{ where } -1 \leq \cos(x) \leq \frac{1}{\sqrt[3]{4}} } $$
Steps to Solve
-
Start with the given equation The equation to be analyzed is: $$ \sin(x) + \sin(x) \cot^2(x) = \sec(x) $$
-
Rewrite cotangent and secant using sine and cosine Recall the definitions:
- $\cot(x) = \frac{\cos(x)}{\sin(x)}$
- $\sec(x) = \frac{1}{\cos(x)}$
Substituting these into the equation gives: $$ \sin(x) + \sin(x) \left( \frac{\cos^2(x)}{\sin^2(x)} \right) = \frac{1}{\cos(x)} $$
-
Simplify the equation This can be rewritten as: $$ \sin(x) + \frac{\cos^2(x)}{\sin(x)} = \frac{1}{\cos(x)} $$ Multiplying through by $\sin(x) \cos(x)$ (noting that we need $x \neq n\pi$ for some integer $n$) provides: $$ \sin^2(x) \cos(x) + \cos^2(x) = \sin(x) $$
-
Rearrange the equation Rearranging gives a polynomial equation in terms of $\sin(x)$: $$ \sin^2(x) \cos(x) - \sin(x) + \cos^2(x) = 0 $$
-
Identify conditions for the solution Letting $u = \sin(x)$ transforms the equation into: $$ u^2 \cos(x) - u + \cos^2(x) = 0 $$
This is a quadratic in $u$, and to have real solutions, the discriminant must be non-negative: $$ D = (-1)^2 - 4 \cos(x) \cos^2(x) $$
-
Set the discriminant greater than or equal to zero For real solutions: $$ 1 - 4\cos^3(x) \geq 0 $$
-
Solve the discriminant inequality This implies: $$ \cos^3(x) \leq \frac{1}{4} $$
The range of $\cos(x)$ is limited by the square root function, leading to: $$ \cos(x) \leq \frac{1}{\sqrt[3]{4}} $$
- Determine the defined range for x As $\cos(x)$ oscillates between -1 and 1, the region of interest must be determined by the solutions to the inequality: $$ -1 \leq \cos(x) \leq \frac{1}{\sqrt[3]{4}} $$
The defined range for $x$ satisfying the equation is: $$ x \in { \text{all } x \text{ where } -1 \leq \cos(x) \leq \frac{1}{\sqrt[3]{4}} } $$
More Information
The range of solutions arises from analyzing the properties of trigonometric functions and using quadratic analysis. The values of $x$ that satisfy this will determine intervals of valid solutions within the cyclic nature of sine and cosine functions.
Tips
- Not considering the periodic nature of trigonometric functions: Always take into account the cycles of sine and cosine when solving trigonometric equations.
- Forgetting that $\cos(x)$ must be within -1 to 1: Solutions that lead to $\cos(x)$ outside this range are invalid.
AI-generated content may contain errors. Please verify critical information