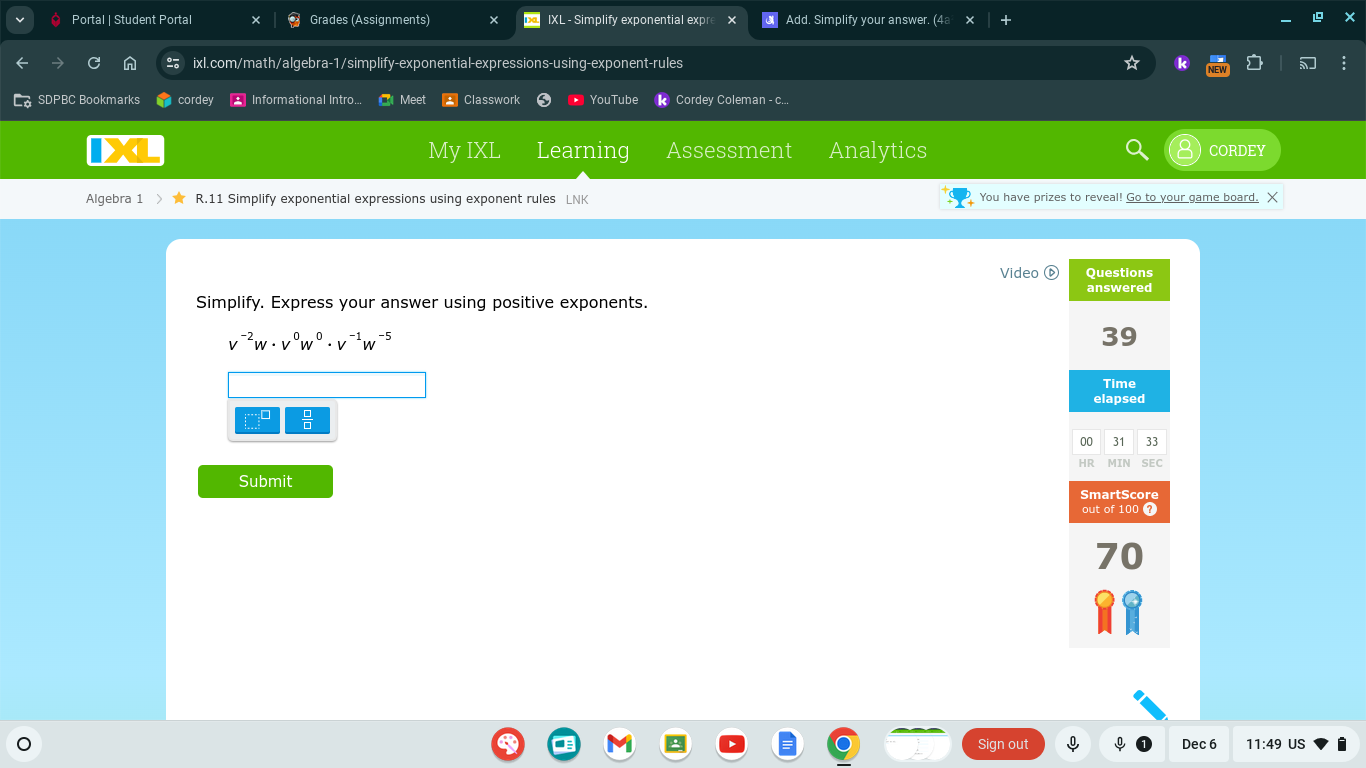
Simplify v^(-2) · w^(0) · w^(0) · v^(-1) · w^(-5). Express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression involving exponents, specifically v to the power of -2, w to the power of 0, w to the power of 0 again, v to the power of -1, and w to the power of -5, while expressing the final answer using only positive exponents.
Answer
$$\frac{1}{v^3 \cdot w^5}$$
Answer for screen readers
The simplified expression is $$\frac{1}{v^3 \cdot w^5}$$
Steps to Solve
-
Identify the expression
The expression to simplify is $v^{-2} \cdot w^{0} \cdot w^{0} \cdot v^{-1} \cdot w^{-5}$.
We note that $w^{0} = 1$, so it won't affect the multiplication. -
Eliminate the zero exponent
Substituting the zero exponents with 1:
$$ v^{-2} \cdot 1 \cdot 1 \cdot v^{-1} \cdot w^{-5} = v^{-2} \cdot v^{-1} \cdot w^{-5}$$ -
Combine the terms with the same base
Use the properties of exponents to combine the terms for $v$:
$$v^{-2} \cdot v^{-1} = v^{-2-1} = v^{-3}$$
So the expression simplifies to:
$$v^{-3} \cdot w^{-5}$$ -
Convert negative exponents to positive
To express the answer using positive exponents, we rewrite the negative exponents:
$$v^{-3} = \frac{1}{v^3} \quad \text{and} \quad w^{-5} = \frac{1}{w^5}$$
Thus,
$$v^{-3} \cdot w^{-5} = \frac{1}{v^3} \cdot \frac{1}{w^5} = \frac{1}{v^3 \cdot w^5}$$
The simplified expression is $$\frac{1}{v^3 \cdot w^5}$$
More Information
This simplification showcases how to manage exponents, particularly negative exponents, ensuring the final result is expressed positively. The concept of exponents is fundamental in algebra, and mastering these rules can significantly aid in various mathematical problems.
Tips
- Ignoring zero exponents: Some may forget that any base raised to the power of zero equals 1.
- Incorrectly combining negative exponents: Remember to add the exponents when multiplying bases with the same base.
AI-generated content may contain errors. Please verify critical information