Simplify the trigonometric expression: cos(30° 32')cos(29° 28') - sin(149° 28')sin(29° 28')
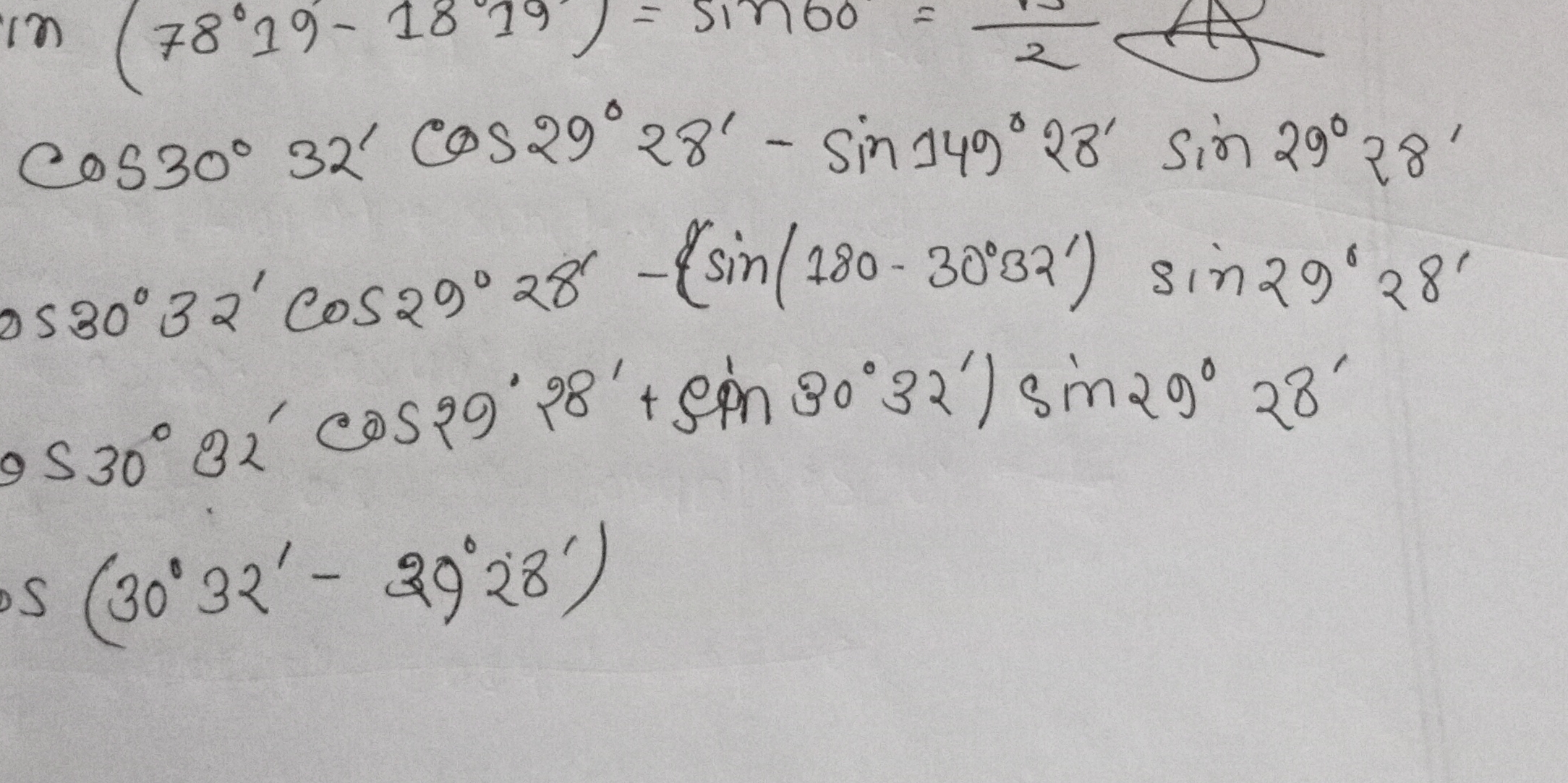
Understand the Problem
The question involves trigonometric identities and simplification. It requires knowledge of trigonometric functions, angle manipulation, and the application of relevant formulas to simplify the expression and solve the problem.
Answer
$\frac{1}{2}$
Answer for screen readers
$\frac{1}{2}$
Steps to Solve
-
Rewrite the expression The expression from the image can be written as: $$ \cos(30^{\circ}32')\cos(29^{\circ}28') - \sin(149^{\circ}28')\sin(29^{\circ}28') $$
-
Use the identity $\sin(180^{\circ} - x) = \sin(x)$ Apply the identity to the sine term: $\sin(149^{\circ}28') = \sin(180^{\circ} - 149^{\circ}28') = \sin(30^{\circ}32')$ $$ \cos(30^{\circ}32')\cos(29^{\circ}28') - \sin(30^{\circ}32')\sin(29^{\circ}28') $$
-
Apply the cosine addition formula Use the cosine addition formula: $\cos(A+B) = \cos A \cos B - \sin A \sin B$. Here, let $A = 30^{\circ}32'$ and $B = 29^{\circ}28'$. $$ \cos(30^{\circ}32' + 29^{\circ}28') $$
-
Simplify the angle Add the angles: $30^{\circ}32' + 29^{\circ}28' = 60^{\circ}$ $$ \cos(60^{\circ}) $$
-
Evaluate the cosine Evaluate $\cos(60^{\circ})$ $$ \cos(60^{\circ}) = \frac{1}{2} $$
$\frac{1}{2}$
More Information
The cosine of $60^{\circ}$ is a commonly known trigonometric value. It's half of an equilateral triangle bisected down the middle, and the ratio of the adjacent side to the hypotenuse is $1/2$.
Tips
A common mistake is incorrectly applying the trigonometric identities, especially the angle addition and subtraction formulas. Another mistake might be in the arithmetic when adding the angles in degrees and minutes.
AI-generated content may contain errors. Please verify critical information