Simplify the following expressions: (x - 1)² - (x - 5)(2x + 3) and 1/2 (2x-8) (3x - 9) - (8 - 3x)
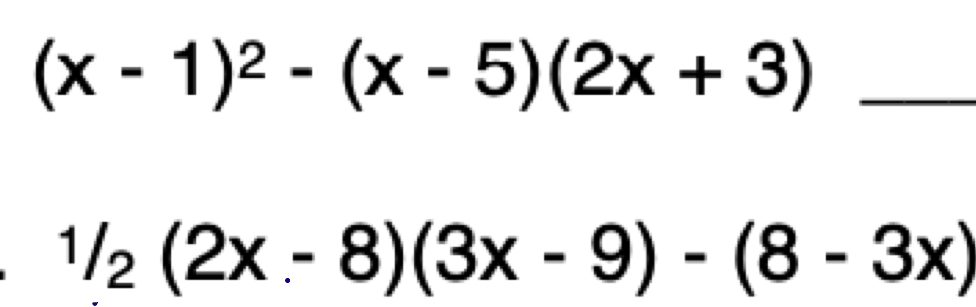
Understand the Problem
The question involves simplifying algebraic expressions. The first expression is "(x - 1)² - (x - 5)(2x + 3)" and likely involves expanding the square, multiplying the binomials, and then combining like terms. The second expression is "1/2 (2x-8) (3x - 9) - (8 - 3x)" and similarly requires distribution and simplification.
Answer
First expression: $-x^2 + 5x + 16$ Second expression: $3x^2 - 18x + 28$
Answer for screen readers
First expression: $-x^2 + 5x + 16$ Second expression: $3x^2 - 18x + 28$
Steps to Solve
- Simplify the first expression: Expand $(x-1)^2$
$(x-1)^2 = x^2 - 2x + 1$
- Simplify the first expression: Expand $(x-5)(2x+3)$
$(x-5)(2x+3) = 2x^2 + 3x - 10x - 15 = 2x^2 - 7x - 15$
- Simplify the first expression: Combine the expanded terms
$(x^2 - 2x + 1) - (2x^2 - 7x - 15) = x^2 - 2x + 1 - 2x^2 + 7x + 15 = -x^2 + 5x + 16$
- Simplify the second expression: Expand $(2x-8)(3x-9)$
$(2x-8)(3x-9) = 6x^2 - 18x - 24x + 72 = 6x^2 - 42x + 72$
- Simplify the second expression: Multiply by $\frac{1}{2}$
$\frac{1}{2} (6x^2 - 42x + 72) = 3x^2 - 21x + 36$
- Simplify the second expression: Distribute the negative sign and combine the expanded terms
$(3x^2 - 21x + 36) - (8 - 3x) = 3x^2 - 21x + 36 - 8 + 3x = 3x^2 - 18x + 28$
First expression: $-x^2 + 5x + 16$ Second expression: $3x^2 - 18x + 28$
More Information
These problems are good practice in expanding polynomials and combining like terms.
Tips
A common mistake is not distributing the negative sign correctly when subtracting polynomials. For example, in the first expression, it is crucial to distribute the negative sign to each term of $2x^2 - 7x - 15$, resulting in $-2x^2 + 7x + 15$. Failing to do so will lead to an incorrect answer. Another common mistake is making errors in multiplying terms or missing terms during expansion.
AI-generated content may contain errors. Please verify critical information