Simplify the following expressions: (a) x * 9x (b) 9bz * b (e) d^4 / (cd^2) (f) k^2*p * 8p^2*k^3 (a) c * 9x * 2xc (c) (3a^3b)^2 (e) -3/8 * (2a^2 / ab) (g) 7wq * (11q^2 + 15hw)
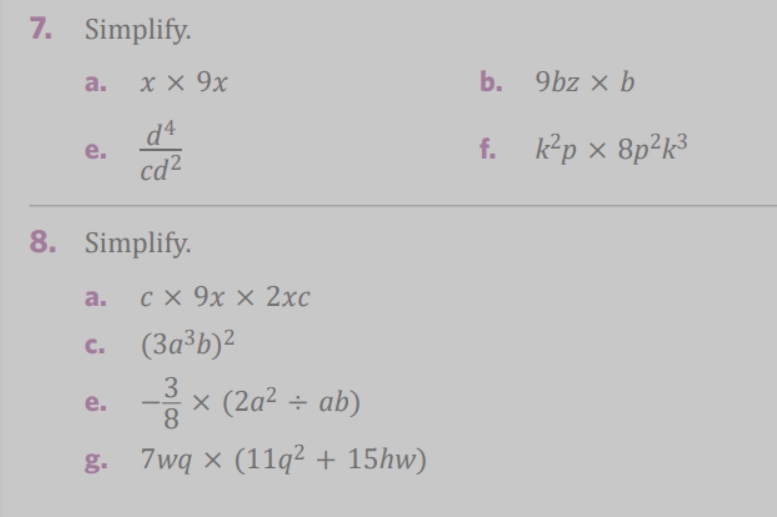
Understand the Problem
The question asks us to 'simplify' several algebraic expressions. This involves combining like terms, applying exponent rules, and performing multiplication and division operations where applicable to reduce the expressions to their simplest forms.
Answer
7a. $9x^2$ 7b. $9b^2z$ 7e. $\frac{d^2}{c}$ 7f. $8k^5p^3$ 8a. $18c^2x^2$ 8c. $9a^6b^2$ 8e. $-\frac{3ax}{4b}$ 8g. $77wq^3 + 105hw^2q$
Answer for screen readers
7a. $9x^2$ 7b. $9b^2z$ 7e. $\frac{d^2}{c}$ 7f. $8k^5p^3$ 8a. $18c^2x^2$ 8c. $9a^6b^2$ 8e. $-\frac{3ax}{4b}$ 8g. $77wq^3 + 105hw^2q$
Steps to Solve
7a. Simplify $x \cdot 9x$ Multiply the coefficients and combine the $x$ terms:
$x \cdot 9x = 9 \cdot x \cdot x = 9x^2$
7b. Simplify $9bz \cdot b$ Multiply the $b$ terms:
$9bz \cdot b = 9 \cdot b \cdot b \cdot z = 9b^2z$
7e. Simplify $\frac{d^4}{cd^2}$ Divide the $d$ terms:
$\frac{d^4}{cd^2} = \frac{d^4}{d^2} \cdot \frac{1}{c} = d^{4-2} \cdot \frac{1}{c} = \frac{d^2}{c}$
7f. Simplify $k^2p \cdot 8p^2k^3$ Multiply the coefficients and combine like terms:
$k^2p \cdot 8p^2k^3 = 8 \cdot k^2 \cdot k^3 \cdot p \cdot p^2 = 8k^{2+3}p^{1+2} = 8k^5p^3$
8a. Simplify $c \cdot 9x \cdot 2xc$ Multiply the coefficients and combine like terms:
$c \cdot 9x \cdot 2xc = 9 \cdot 2 \cdot c \cdot c \cdot x \cdot x = 18c^2x^2$
8c. Simplify $(3a^3b)^2$ Apply the power to each term inside the parentheses:
$(3a^3b)^2 = 3^2 \cdot (a^3)^2 \cdot b^2 = 9 \cdot a^{3 \cdot 2} \cdot b^2 = 9a^6b^2$
8e. Simplify $-\frac{3}{8}x \cdot (2a^2 \div ab)$ Simplify inside the parentheses first. Note that $2a^2 \div ab = \frac{2a^2}{ab} = \frac{2a}{b}$. Then, multiply by $-\frac{3}{8}x$:
$-\frac{3}{8}x \cdot \frac{2a}{b} = -\frac{3 \cdot 2}{8} \cdot \frac{ax}{b} = -\frac{6}{8} \cdot \frac{ax}{b} = -\frac{3}{4} \cdot \frac{ax}{b} = -\frac{3ax}{4b}$
8g. Simplify $7wq \cdot (11q^2 + 15hw)$ Distribute the $7wq$ term:
$7wq \cdot (11q^2 + 15hw) = 7wq \cdot 11q^2 + 7wq \cdot 15hw = 7 \cdot 11 \cdot w \cdot q \cdot q^2 + 7 \cdot 15 \cdot w \cdot q \cdot h \cdot w = 77wq^3 + 105hw^2q$
7a. $9x^2$ 7b. $9b^2z$ 7e. $\frac{d^2}{c}$ 7f. $8k^5p^3$ 8a. $18c^2x^2$ 8c. $9a^6b^2$ 8e. $-\frac{3ax}{4b}$ 8g. $77wq^3 + 105hw^2q$
More Information
These simplifications use the basic rules of algebra, including combining like terms, using exponent rules, and distributing terms in parentheses.
Tips
A common mistake is not correctly applying the exponent rules or not distributing terms correctly. Another common mistake is not combining like terms correctly. For example, in 7f, it is important to add the exponents of the $k$ terms and $p$ terms separately. In 8g, failing to distribute $7wq$ to both terms inside the parentheses is a common mistake. Also, remember that when dividing terms with exponents, you subtract the exponents (as in 7e). When multiplying, exponents of like variables are summed (as in 7f and 8a).
AI-generated content may contain errors. Please verify critical information