Simplify the following expression: (9m^7 - 27m^3 + 81m^2) / (18m^3)
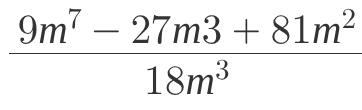
Understand the Problem
The question asks to simplify a rational expression. We will factor out common terms from the numerator and then simplify the expression by dividing out common factors.
Answer
$\frac{m^5 - 3m + 9}{2m}$
Answer for screen readers
$\frac{m^5 - 3m + 9}{2m}$
Steps to Solve
- Factor out the greatest common factor (GCF) from the numerator
The GCF of $9m^7$, $-27m^3$, and $81m^2$ is $9m^2$. Factoring this out, we get: $$ \frac{9m^2(m^5 - 3m + 9)}{18m^3} $$
- Simplify the fraction by canceling common factors
We can simplify the numerical coefficients by dividing both numerator and denominator by 9: $$ \frac{9m^2(m^5 - 3m + 9)}{18m^3} = \frac{m^2(m^5 - 3m + 9)}{2m^3} $$ Now, we simplify the variable terms by dividing both numerator and denominator by $m^2$: $$ \frac{m^2(m^5 - 3m + 9)}{2m^3} = \frac{m^5 - 3m + 9}{2m} $$
$\frac{m^5 - 3m + 9}{2m}$
More Information
The simplified form of the given rational expression is $\frac{m^5 - 3m + 9}{2m}$. We factored out the greatest common factor from the numerator and then simplified the fraction.
Tips
A common mistake includes incorrectly identifying the greatest common factor, which will make the simplification process more difficult. Another mistake is not completely simplifying the expression. For example, only simplifying the coefficients and forgetting about the variables, or vice versa.
AI-generated content may contain errors. Please verify critical information