Simplify the following expression: 1/2 * (2x - 8) * (3x - 9) - (8 - 3x)
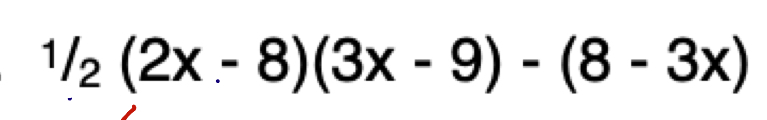
Understand the Problem
The question requires us to simplify and evaluate an algebraic expression. This involves distributing, combining like terms, and simplifying the final result. The expression contains terms with 'x' and constant terms.
Answer
$3x^2 - 18x + 28$
Answer for screen readers
$3x^2 - 18x + 28$
Steps to Solve
-
Expand the first two binomials Expand $(2x - 8)(3x - 9)$ using the distributive property (FOIL method): $$(2x - 8)(3x - 9) = (2x)(3x) + (2x)(-9) + (-8)(3x) + (-8)(-9) = 6x^2 - 18x - 24x + 72 = 6x^2 - 42x + 72$$
-
Multiply by $\frac{1}{2}$ Multiply the result from step 1 by $\frac{1}{2}$: $$\frac{1}{2}(6x^2 - 42x + 72) = 3x^2 - 21x + 36$$
-
Distribute the negative sign Distribute the negative sign in front of the parentheses: $$-(8 - 3x) = -8 + 3x$$
-
Combine the results Combine the results from step 2 and step 3: $$(3x^2 - 21x + 36) + (-8 + 3x) = 3x^2 - 21x + 3x + 36 - 8 = 3x^2 - 18x + 28$$
$3x^2 - 18x + 28$
More Information
The simplified form of the given expression is $3x^2 - 18x + 28$.
Tips
- Incorrectly distributing the $\frac{1}{2}$: Forgetting to multiply every term inside the parentheses by $\frac{1}{2}$ is a common error.
- Sign errors: Mistakes in distributing the negative sign in the expression $-(8-3x)$ are also frequent.
- Combining unlike terms: Combining $x^2$ terms with $x$ or constant terms.
AI-generated content may contain errors. Please verify critical information