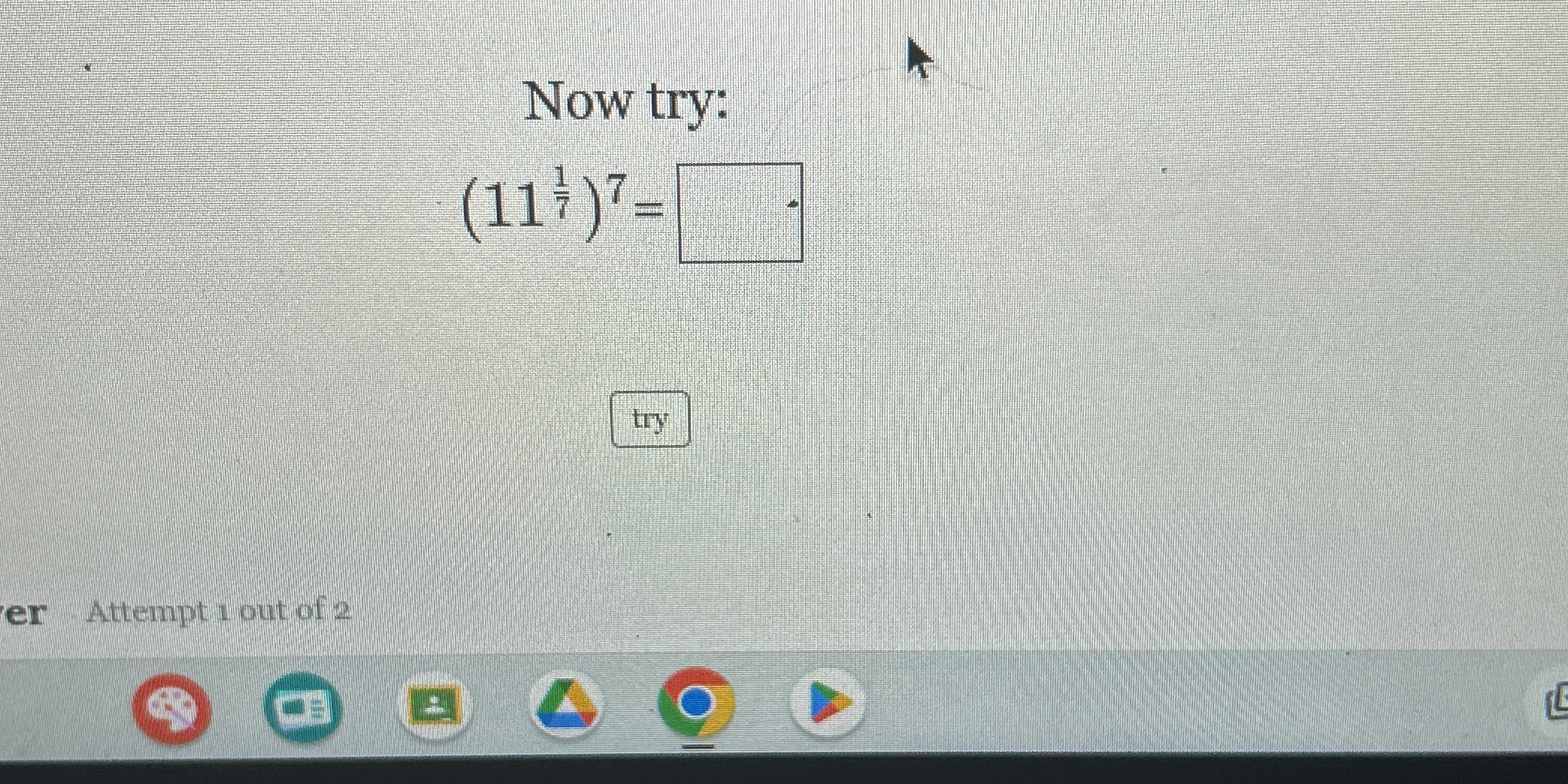
Simplify the following expression: (11^(1/7))^7
Understand the Problem
The question asks to simplify the expression (11^(1/7))^7. To simplify the expression, we can use the power of a power rule which says (a^m)^n = a^(m*n), where a is the base and m and n are the exponents.
Answer
$11$
Answer for screen readers
$11$
Steps to Solve
- Apply the power of a power rule
To simplify the expression $(11^{\frac{1}{7}})^7$, we use the rule $(a^m)^n = a^{m \cdot n}$. So we need to multiply the exponents $\frac{1}{7}$ and $7$.
- Multiply the exponents
Multiply $\frac{1}{7}$ by $7$:
$$ \frac{1}{7} \cdot 7 = \frac{7}{7} = 1 $$
- Simplify the expression
Substitute the result back into the expression:
$11^1 = 11$
$11$
More Information
Any number raised to the power of 1 is equal to the number itself.
Tips
- Forgetting to multiply the exponents.
- Incorrectly multiplying the fractions.
AI-generated content may contain errors. Please verify critical information
Thank you for voting!
