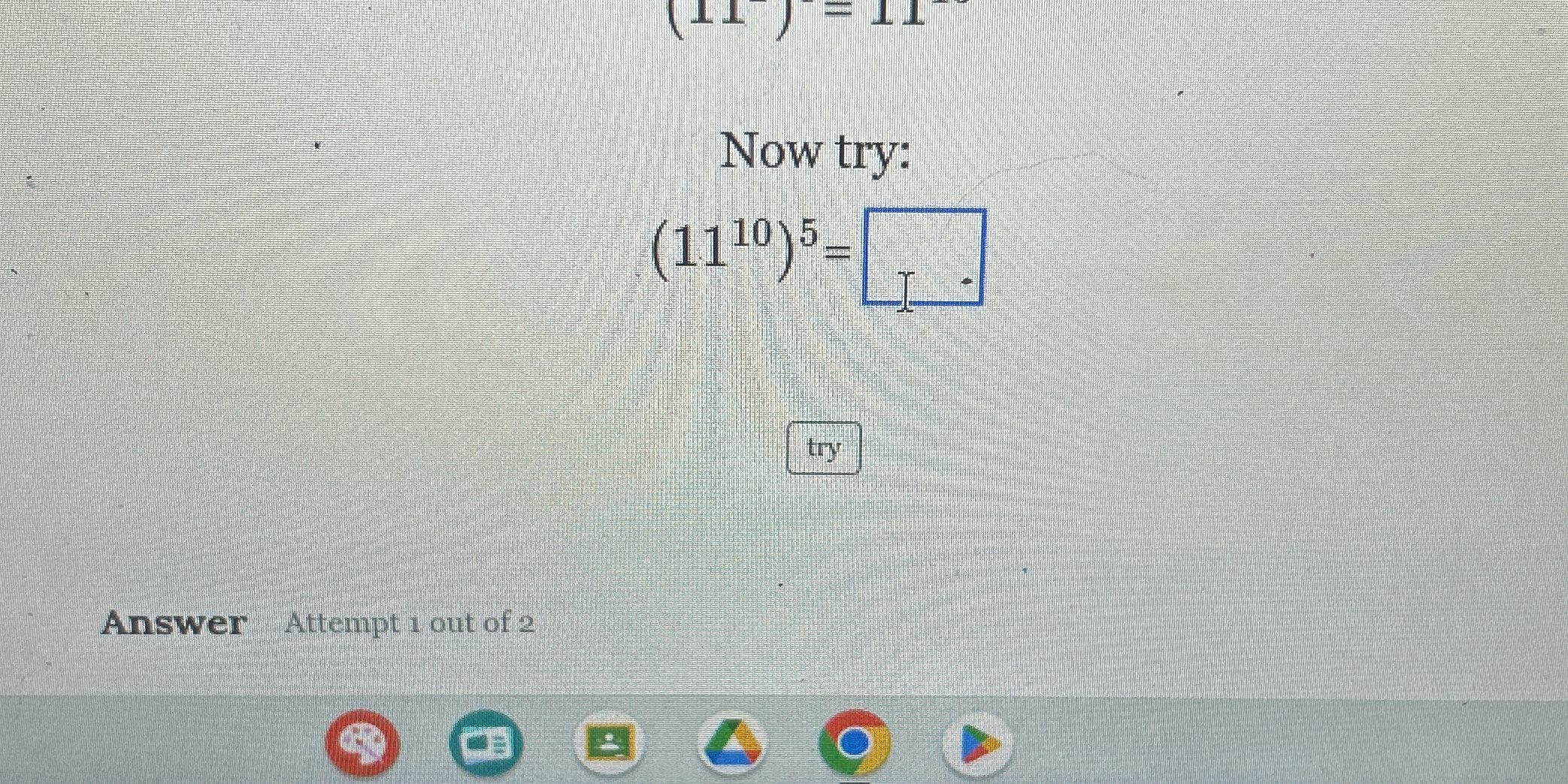
Simplify the following expression: (11^10)^5
Understand the Problem
The question is asking to simplify the expression (11^10)^5 using the power of a power rule. The power of a power rule states that (a^m)^n = a^(m*n), where 'a' is the base and 'm' and 'n' are exponents. We need to multiply exponents together.
Answer
$11^{50}$
Answer for screen readers
$11^{50}$
Steps to Solve
-
Apply the power of a power rule The power of a power rule states that $(a^m)^n = a^{m \cdot n}$. Therefore, we have $(11^{10})^5 = 11^{10 \cdot 5}$.
-
Multiply the exponents Multiply the exponents $10$ and $5$ to get $10 \cdot 5 = 50$.
-
Write the simplified expression Substitute the result from step 2 into the expression: $11^{10 \cdot 5} = 11^{50}$.
$11^{50}$
More Information
The power of a power rule is a fundamental property of exponents used to simplify expressions. When raising a power to another power, you simply multiply the exponents together while keeping the base the same.
Tips
A common mistake is to add the exponents instead of multiplying them. Remember that $(a^m)^n = a^{m \cdot n}$, not $a^{m+n}$. Another mistake could be changing the base to the product of the base with one of its exponents.
AI-generated content may contain errors. Please verify critical information